
”¾ĢāÄæ”æĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£Ø””””£©
A. ĪŖĮĖ½āČ«Ź”֊ѧɜµÄŠÄĄķ½”æµ×“æö£¬ŅĖ²ÉÓĆĘղ鷽Ź½
B. ÖĄĮ½Ć¶ÖŹµŲ¾łŌȵÄÓ²±Ņ£¬Į½Ć¶Ó²±Ņ¶¼ŹĒÕżĆę³ÆÉĻÕāŅ»ŹĀ¼ž·¢ÉśµÄøÅĀŹĪŖ![]()
C. ÖĄŅ»Ć¶ÖŹµŲ¾łŌȵÄÕż·½Ģå÷»×Ó£¬÷»×ÓĶ£Ö¹×Ŗ¶Æŗó£¬5µć³ÆÉĻŹĒ±ŲČ»ŹĀ¼ž
D. ¼×ŅŅĮ½ČĖŌŚĻąĶ¬Ģõ¼žĻĀø÷Éä»÷10“Ī£¬ĖūĆĒ³É¼ØµÄĘ½¾łŹżĻąĶ¬£¬·½²ī·Ö±šŹĒS¼×2£½0.4£¬SŅŅ2£½0.6£¬Ōņ¼×µÄÉä»÷³É¼Ø½ĻĪȶØ
”¾“š°ø”æD
”¾½āĪö”æ
øł¾Żµ÷²éÓė³éŃłµ÷²é”¢·½²īµÄŠŌÖŹŅŌ¼°Ė껜ŹĀ¼žÓė±ŲČ»ŹĀ¼žµÄ¶ØŅ弓æɵƵ½½įĀŪ£®
½ā£ŗA”¢ĪŖĮĖ½āČ«Ź”֊ѧɜµÄŠÄĄķ½”æµ×“æö£¬ŅĖ²ÉÓĆ³é²é·½Ź½£¬¹Ź“ķĪó£»
B”¢ÖĄĮ½Ć¶ÖŹµŲ¾łŌȵÄÓ²±Ņ£¬Į½Ć¶Ó²±Ņ¶¼ŹĒÕżĆę³ÆÉĻÕāŅ»ŹĀ¼ž·¢ÉśµÄøÅĀŹĪŖ![]() £»¹Ź“ķĪó£»
£»¹Ź“ķĪó£»
C”¢ÖĄŅ»Ć¶ÖŹµŲ¾łŌȵÄÕż·½Ģå÷»×Ó£¬÷»×ÓĶ£Ö¹×Ŗ¶Æŗó£¬5µć³ÆÉĻŹĒĖ껜ŹĀ¼ž£»¹Ź“ķĪó£»
D”¢¼×ŅŅĮ½ČĖŌŚĻąĶ¬Ģõ¼žĻĀø÷Éä»÷10“Ī£¬ĖūĆĒ³É¼ØµÄĘ½¾łŹżĻąĶ¬£¬·½²ī·Ö±šŹĒS¼×2£½0.4£¬SŅŅ2£½0.6£¬Ōņ¼×µÄÉä»÷³É¼Ø½ĻĪČ¶Ø£¬¹ŹÕżČ·£»
¹ŹŃ”£ŗD£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
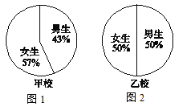
”¾ĢāÄæ”æČēĶ¼1ŗĶČēĶ¼2·Ö±šŹĒ±ķŹ¾¼×”¢ŅŅĮ½ĖłŃ§Š£ÄŠ”¢Å®Éś±ČĄżµÄĶ³¼ĘĶ¼£¬ĒėÅŠ¶ĻĻĀĮŠĖµ·ØŹĒ·ńÕżČ·£¬²¢ĖµĆ÷ĄķÓÉ£®
(1)¼×Š£µÄÅ®ÉśČĖŹż±ČÄŠÉśČĖŹż¶ą£®
(2)ŅŅŠ£µÄÄŠ”¢Å®ÉśČĖŹżŅ»Ńł¶ą£®
(3)¼×Š£Å®ÉśČĖŹż±ČŅŅŠ£Å®ÉśČĖŹż¶ą£®
(4)²»ÄÜ±Č½ĻĮ½øöѧŠ£Å®ÉśČĖŹżµÄ¶ąÉŁ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒijŹŠĮ¬Šų5ĢģµÄĢģĘųĒéæö£®

£Ø1£©ĄūÓĆ·½²īÅŠ¶ĻøĆŹŠÕā5ĢģµÄČÕ×īøßĘųĪĀ²Ø¶Æ“ó»¹ŹĒČÕ×īµĶĘųĪĀ²Ø¶Æ“ó£»
£Ø2£©øł¾ŻČēĶ¼Ģį¹©µÄŠÅĻ¢£¬ĒėŌŁŠ“³öĮ½øö²»Ķ¬ĄąŠĶµÄ½įĀŪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ×ŪŗĻÓėĢ½¾æ£ŗ
ČēĶ¼1£¬Å×ĪļĻßy£½x2+![]() x+3ÓėxÖį½»ÓŚC”¢FĮ½µć£ØµćCŌŚµćF×ó±ß£©£¬ÓėyÖį½»ÓŚµćD£¬AD£½2£¬µćB×ų±źĪŖ£Ø©4£¬5£©£¬µćEĪŖABÉĻŅ»µć£¬ĒŅBE£½ED£¬Į¬½ÓCD£¬CB£¬CE£®
x+3ÓėxÖį½»ÓŚC”¢FĮ½µć£ØµćCŌŚµćF×ó±ß£©£¬ÓėyÖį½»ÓŚµćD£¬AD£½2£¬µćB×ų±źĪŖ£Ø©4£¬5£©£¬µćEĪŖABÉĻŅ»µć£¬ĒŅBE£½ED£¬Į¬½ÓCD£¬CB£¬CE£®
£Ø1£©ĒóµćC”¢D”¢EµÄ×ų±ź£»
£Ø2£©ČēĶ¼2£¬ŃÓ³¤ED½»xÖįÓŚµćM£¬ĒėÅŠ¶Ļ”÷CEMµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ŌŚĶ¼2µÄ»ł“”ÉĻ£¬½«”÷CEMŃŲ×ÅCE·ÕŪ£¬Ź¹µćMĀäŌŚµćM'“¦£¬ĒėÅŠ¶ĻµćM'ŹĒ·ńŌŚ“ĖÅ×ĪļĻßÉĻ£¬²¢ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
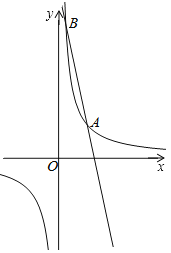
”¾ĢāÄæ”æČēĶ¼£¬·“±ČĄżŗÆŹży1£½![]() ÓėŅ»“ĪŗÆŹży2£½ax+bµÄĶ¼Ļó½»ÓŚµćA£Ø2£¬2£©”¢B£Ø
ÓėŅ»“ĪŗÆŹży2£½ax+bµÄĶ¼Ļó½»ÓŚµćA£Ø2£¬2£©”¢B£Ø![]() £¬n£©£®
£¬n£©£®
£Ø1£©ĒóÕāĮ½øöŗÆŹż½āĪöŹ½£»
£Ø2£©Ö±½ÓŠ“³ö²»µČŹ½y2£¾1yµÄ½ā¼Æ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
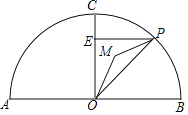
”¾ĢāÄæ”æČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬ĒŅAO£½4£¬µćCŌŚ°ėŌ²ÉĻ£¬OC”ĶAB£¬“¹×ćĪŖµćO£¬PĪŖ°ėŌ²ÉĻČĪŅāŅ»µć¹żPµć×÷PE”ĶOCÓŚµćE£¬Éč”÷OPEµÄÄŚŠÄĪŖM£¬Į¬½ÓOM
£Ø1£©Ēó”ĻOMPµÄ¶ČŹż£»
£Ø2£©Ėę×ŵćPŌŚ°ėŌ²ÉĻĪ»ÖƵÄøı䣬”ĻCMOµÄ“󊔏Ē·ńøı䣬ĖµĆ÷ĄķÓÉ£»
£Ø3£©µ±µćPŌŚ°ėŌ²ÉĻ“ÓµćBŌĖ¶Æµ½µćAŹ±£¬Ö±½ÓŠ“³öÄŚŠÄMĖł¾¹żµÄĀ·¾¶³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
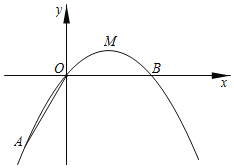
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¶„µćĪŖMµÄÅ×ĪļĻßC1£ŗy£½ax2+bx£Øa£¼0£©¾¹żµćAŗĶxÖįÉĻµÄµćB£¬AO£½OB£½2£¬”ĻAOB£½120”ć£®
£Ø1£©ĒóøĆÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©ĮŖ½įAM£¬ĒóS”÷AOM£»
£Ø3£©½«Å×ĪļĻßC1ĻņÉĻĘ½ŅʵƵ½Å×ĪļĻßC2£¬Å×ĪļĻßC2ÓėxÖį·Ö±š½»ÓŚµćE”¢F£ØµćEŌŚµćFµÄ×ó²ą£©£¬Čē¹ū”÷MBFÓė”÷AOMĻąĖĘ£¬ĒóĖłÓŠ·ūŗĻĢõ¼žµÄÅ×ĪļĻßC2µÄ±ķ“ļŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉ趞“ĪŗÆŹż![]() £Ø
£Ø![]() ”¢
”¢![]() ŹĒŹµŹż£©.
ŹĒŹµŹż£©.
¢Å¼×ĒóµĆµ±![]() Ź±£¬
Ź±£¬![]() £»µ±
£»µ±![]() Ź±£¬
Ź±£¬![]() £¬ŅŅĒóµĆµ±
£¬ŅŅĒóµĆµ±![]() Ź±£¬
Ź±£¬![]() .Čō¼×ĒóµĆµÄ½į¹ū¶¼ÕżČ·£¬ÄćČĻĪŖŅŅĒóµĆµÄ½į¹ūÕżČ·Āš£æĖµĆ÷ĄķÓÉ£»
.Čō¼×ĒóµĆµÄ½į¹ū¶¼ÕżČ·£¬ÄćČĻĪŖŅŅĒóµĆµÄ½į¹ūÕżČ·Āš£æĖµĆ÷ĄķÓÉ£»
¢ĘŠ“³ö¶ž“ĪŗÆŹżµÄ¶Ō³ĘÖį£¬²¢Ēó³öøĆŗÆŹżµÄ×īŠ”Öµ£ØÓĆŗ¬![]() ”¢
”¢![]() µÄ“śŹżŹ½±ķŹ¾£©£»
µÄ“śŹżŹ½±ķŹ¾£©£»
¢ĒŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼Ļń¾¹ż![]() £¬
£¬![]() Į½µć£Øm”¢nŹĒŹµŹż£©£¬µ±
Į½µć£Øm”¢nŹĒŹµŹż£©£¬µ±![]() Ź±£¬ĒóÖ¤£ŗ
Ź±£¬ĒóÖ¤£ŗ![]() .
.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
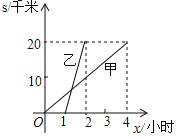
”¾ĢāÄæ”æŅŃÖŖA”¢BĮ½µŲÖ®¼äµÄ¾ąĄėĪŖ20Ē§Ć×£¬¼×²½ŠŠ£¬ŅŅĘļ³µ£¬Į½ČĖŃŲ×ÅĻąĶ¬Ā·Ļߣ¬ÓÉAµŲµ½BµŲŌČĖŁĒ°ŠŠ£¬¼×”¢ŅŅŠŠ½ųµÄĀ·³ĢsÓėx£ØŠ”Ź±£©µÄŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£®£Ø1£©ŅŅ±Č¼×Ķķ³ö·¢___Š”Ź±£»£Ø2£©ŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬¼×”¢ŅŅĮ½ČĖÖ®¼äµÄ¾ąĄėĖęxµÄŌö“ó¶ųŌö“óŹ±£¬xµÄȔֵ·¶Ī§ŹĒ___£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com