
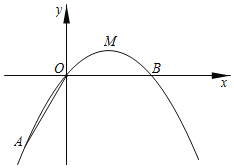
【题目】如图,在平面直角坐标系中,顶点为M的抛物线C1:y=ax2+bx(a<0)经过点A和x轴上的点B,AO=OB=2,∠AOB=120°.
(1)求该抛物线的表达式;
(2)联结AM,求S△AOM;
(3)将抛物线C1向上平移得到抛物线C2,抛物线C2与x轴分别交于点E、F(点E在点F的左侧),如果△MBF与△AOM相似,求所有符合条件的抛物线C2的表达式.
【答案】(1)y=![]() ;(2)S△AOM=
;(2)S△AOM=![]() ;(3)y=
;(3)y=![]() ;y=
;y=![]() .
.
【解析】
(1)根据题意,可以写出点B和点A的坐标,从而可以得到该抛物线的表达式;
(2)根据(1)中的函数解析式,可以求得点M的坐标,从而可以求得直线AM的函数解析式,从而可以求得S△AOM;
(3)根据题意,利用分类讨论的方法和三角形相似的知识可以求得点F的坐标,从而可以求得抛物线C2的表达式.
(1)∵抛物线C1:y=ax2+bx(a<0)经过点A和x轴上的点B,AO=OB=2,∠AOB=120°,
∴点B(2,0),点A(﹣1,﹣![]() ),
),
∴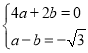 ,
,
得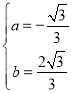 ,
,
∴该抛物线的解析式为y=![]() ;
;
(2)连接MO,AM,AM与y轴交于点D,
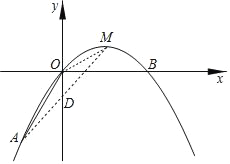
∵y=![]() =
=![]() ,
,
∴点M的坐标为(1,![]() ),
),
设过点A(﹣1,﹣![]() ),M(1,
),M(1,![]() )的直线解析式为y=mx+n,
)的直线解析式为y=mx+n,
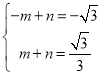 ,得
,得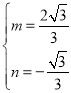 ,
,
∴直线AM的函数解析式为y=![]() x﹣
x﹣![]() ,
,
当x=0时,y=﹣![]() ,
,
∴点D的坐标为(0,﹣![]() ),
),
∴OD=![]() ,
,
∴S△AOM=S△AOD+S△MOD= ;
;
(3)当△AOM∽△FBM时,![]() ,
,
∵OA=2,点O(0,0),点M(1,![]() ),点B(2,0),
),点B(2,0),
∴OM=![]() ,BM=
,BM=![]() ,
,
∴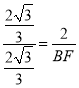 ,
,
解得,BF=2,
∴点F的坐标为(4,0),
设抛物线C2的函数解析式为:y=![]() +c,
+c,
∵点F(4,0)在抛物线C2上,
∴0=![]() +c,得c=
+c,得c=![]() ,
,
∴抛物线C2的函数解析式为:y=![]() +
+![]() ;
;
当△AOM∽△MBF时,
![]() ,
,
∵OA=2,点O(0,0),点M(1,![]() ),点B(2,0),
),点B(2,0),
∴OM=![]() ,BM=
,BM=![]() ,
,
∴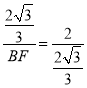 ,
,
解得,BF=![]() ,
,
∴点F的坐标为(![]() ,0),
,0),
设抛物线C2的函数解析式为:y=![]() +d,
+d,
∵点F(![]() ,0)在抛物线C2上,
,0)在抛物线C2上,
∴0=![]() ,得d=
,得d=![]() ,
,
∴抛物线C2的函数解析式为:y=![]() +
+![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】结论开放某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行调查.依据所有调查数据绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
类别 | 人数 | 占总人数的比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | c |
说不清楚 | 9 | 0.06 |

(1)求样本容量及表格中a,b,c的值,并补全统计图.
(2)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
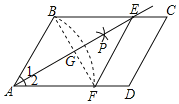
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 为了解全省中学生的心理健康状况,宜采用普查方式
B. 掷两枚质地均匀的硬币,两枚硬币都是正面朝上这一事件发生的概率为![]()
C. 掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
D. 甲乙两人在相同条件下各射击10次,他们成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
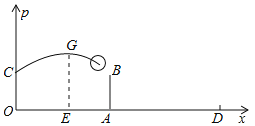
【题目】为如图,已知女排球场的长度OD为18米,位于球场中线处的球网AB的高度2.24米,一队员站在点O处发球,排球从点O的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为6米时,到达最高点G,以O为原点建立如图所示的平面直角坐标系.
(1)若排球运行的最大高度为2.8米,求排球飞行的高度p(单位:米)与水平距离x(单位:米)之间的函数关系式(不要求写自变量x的取值范围);
(2)在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由;
(3)若李明同学发球要想过网,又使排球不会出界(排球压线属于没出界)求二次函数中二次项系数的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )

A. (3,4)或(2,4) B. (2,4)或(8,4)
C. (3,4)或(8,4) D. (3,4)或(2,4)或(8,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为![]() 点,D点的对称点为
点,D点的对称点为![]() 点,若
点,若![]() ,
,![]() 的面积为4,
的面积为4,![]() 的面积为1,则矩形ABCD的面积等于_____.
的面积为1,则矩形ABCD的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A、B在x轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=
(k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=![]() ,则k的值_____.
,则k的值_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
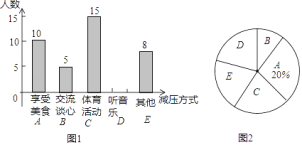
![]() 九年级接受调查的同学共有多少名,并补全条形统计图;
九年级接受调查的同学共有多少名,并补全条形统计图;
![]() 九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
![]() 若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com