
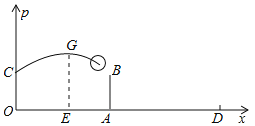
����Ŀ��Ϊ��ͼ����֪Ů���ij���ODΪ18�ף�λ�������ߴ�������AB�ĸ߶�2.24�ף�һ��Ավ�ڵ�O����������ӵ�O�����Ϸ�2��C������ǰ����ȥ������ķ���·���������ߵ�һ���֣����������������O��ˮƽ����OEΪ6��ʱ��������ߵ�G����OΪԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ��
��1�����������е����߶�Ϊ2.8�ף���������еĸ߶�p����λ���ף���ˮƽ����x����λ���ף�֮��ĺ�����ϵʽ����Ҫ��д�Ա���x��ȡֵ��Χ����
��2���ڣ�1���������£�������������ܹ�����������ܹ��������Ƿ����磿��˵�����ɣ�
��3��������ͬѧ����Ҫ���������ʹ������磨����ѹ������û���磩����κ����ж�����ϵ�������ֵ��
���𰸡���1��p��![]() ��x��6��2+2.8;��2��������;��3��
��x��6��2+2.8;��2��������;��3��![]() .
.
��������
��1�����������ߵĶ�������Ϊ��6��2.8�������㣨0��2���������ʽ�������
��2�����õ�x��9ʱ��x��18ʱ���ֱ����pֵ�����ж�
��3���������ߵĽ���ʽΪ��p��a��x��6��2+h������C���룬��ʱ�����ߵĽ���ʽΪp��a��x��6��2+2��36a���ٸ���x��9ʱ��p��2.24����x��18ʱ��p��0�����ɵ�a�ķ�Χ���Ӷ�ȡ�����ֵ��
�⣺
��1�����������е����߶�Ϊ28�ף���������GΪ��6��2.8�������������ߵĽ���ʽΪp��a��x��6��2+2.8
�ߵ�C����Ϊ��0��2������C����������
��2��a��0��6��2+2.8
���a����![]()
��p��-![]() ��x��6��2+2.8
��x��6��2+2.8
��������еĸ߶�p����λ���ף���ˮƽ����x����λ���ף�֮��ĺ�����ϵʽ��p��-![]() ��x��6��2+2.8
��x��6��2+2.8
��2����x��9ʱ��
p��-![]() ��9��6��2+2.8��2.6��2.24
��9��6��2+2.8��2.6��2.24
��x��18ʱ��
p��-![]() ��18��6��2+2.8����0.4��0
��18��6��2+2.8����0.4��0
����η�����Թ����Ҳ����߽�
��3���������ߵĽ���ʽΪ��p��a��x��6��2+h��
����C����ã�36a+h��2����h��2��36a
���ʱ�����ߵĽ���ʽΪ
p��a��x��6��2+2��36a
�������⣬�����߽�ʱ�У�a��18��6��2+2��36a��0�����a��-![]()
Ҫʹ���������a��9��6��2+2��36a��2.24�����a��![]()
������ͬѧ����Ҫ���������ʹ������磨����ѹ������û���磩���κ����ж�����ϵ�������ֵΪ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
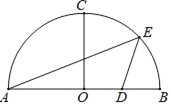
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ�����뾶OC��AB��OB��4��D��OB���е㣬��E�ǻ�BC�ϵĶ��㣬����AE�� DE��
��1������E�ǻ�BC���е�ʱ������ADE�������
��2����tan��AED��![]() ����AE�ij���
����AE�ij���
��3����F�ǰ뾶OC��һ���㣬���E��ֱ��OC�ľ���Ϊm��
�ٵ���DEF�ǵ���ֱ��������ʱ����m��ֵ��
���ӳ�DF����Բ���ڵ�G������AG����EG��AG��DE��ֱ��д��DE�ij��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
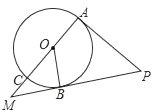
����Ŀ����ͼ��AC�ǡ�O��ֱ����OB�ǡ�O�İ뾶��PA�С�O�ڵ�A��PB��AC���ӳ��߽��ڵ�M����COB����APB��
��1����֤��PB�ǡ�O�����ߣ�
��2����MB��4��MC��2ʱ�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
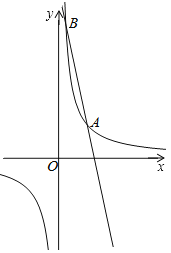
����Ŀ����ͼ������������y1��![]() ��һ�κ���y2��ax+b��ͼ���ڵ�A��2��2����B��
��һ�κ���y2��ax+b��ͼ���ڵ�A��2��2����B��![]() ��n����
��n����
��1������������������ʽ��
��2��ֱ��д������ʽy2��1y�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
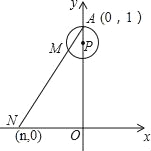
����Ŀ����ͼ����ֱ������ϵxOy�У���֪��A��0��1������P���߶�OA�ϣ���APΪ�뾶�ġ�P�ܳ�Ϊ1����M��A��ʼ�ء�P����ʱ�뷽��ת��������AM��x���ڵ�N��n��0�������Mת����·��Ϊm��0��m��1����
��1����m=![]() ʱ��n=_____��
ʱ��n=_____��
��2�����ŵ�M��ת������m��![]() �仯��
�仯��![]() ʱ����N��Ӧ�ƶ���·����Ϊ_____��
ʱ����N��Ӧ�ƶ���·����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
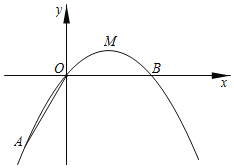
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ΪM��������C1��y��ax2+bx��a��0��������A��x���ϵĵ�B��AO��OB��2����AOB��120�㣮
��1����������ߵı���ʽ��
��2������AM����S��AOM��
��3����������C1����ƽ�Ƶõ�������C2��������C2��x��ֱ��ڵ�E��F����E�ڵ�F����ࣩ�������MBF���AOM���ƣ������з���������������C2�ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧУ��֯�ġ�ѧϰǿ�����Ķ�֪ʶ�����У�ÿ��μӱ�����������ͬ���ɼ���ΪA��B��C��D�ĸ��ȼ���������Ӧ�ȼ��ĵ÷����μ�Ϊ100�֣�90�֣�80�ֺ�70�֣��꼶�鳤����ʦ��901���902��ijɼ��������������Ƴ����µ�ͳ��ͼ��
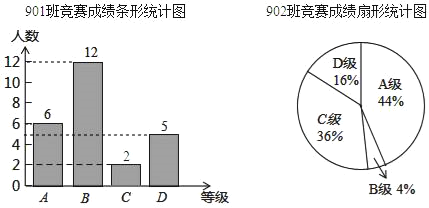
(1)�ڱ��ξ����У�902��C�������ϵ������ж��٣�
(2)���㽫����ı���������
ƽ����(��) | ��λ��(��) | ����(��) | B������������ | |
901�� | 87.6 | 90 | �� �� | 18 |
902�� | 87.6 | �� �� | 100 | �� �� |
(3)�����901���902���ڱ��ξ����еijɼ����бȽϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������A��B����Ʒ��̨�ƣ�����Aÿյ���۱�B���۹�30Ԫ��A�ۼ�120Ԫ��B�ۼ�80Ԫ.��֪��1040Ԫ������A��������650Ԫ����B��������ͬ.
��1����A��B�Ľ��ۣ�
��2�����д��㹺��A��B̨�ƹ�100յ��Ҫ��A��B������������3400Ԫ�����ö���3550Ԫ�����ж����ֽ���������
��3���ڣ�2���������£��ó��о�����A���н��۴�����Ą��ÿյ����m��8��m��15��Ԫ��B���䣬������ν����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABOC����һ��OB��x���ϣ�������ABOC�Ƶ�B˳ʱ����ת75����FBDE��λ�ã���BO��2����A��120�������E������Ϊ��������
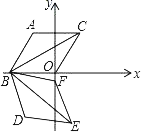
A. ��![]() ��B. ��
��B. ��![]() ��C. ��
��C. ��![]() ��D. ��
��D. ��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com