
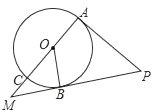
【题目】如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
(1)求证:PB是⊙O的切线;
(2)当MB=4,MC=2时,求⊙O的半径.
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1.有下列4个结论:①abc>0;②4a+2b+c>0;③2c<3b;④a+b>m(am+b)(m是不等于1的实数).其中正确的结论个数有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
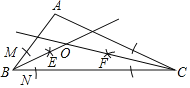
【题目】如图,在△ABC中,按以下步骤作图:
①以B为圆心,任意长为半径作弧,分别交AB.BC于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点E;③作射线BE;④用同样的方法作射线CF.BE交CF于点O.
MN的长为半径作弧,两弧相交于点E;③作射线BE;④用同样的方法作射线CF.BE交CF于点O.
请根据作图回答下列问题:
(1)O是△ABC的 ;
A.外心 B.内心 C.重心
(2)若AB=5,AC=12,BC=13,求O到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
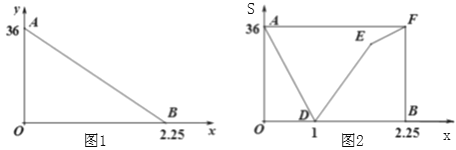
【题目】“低碳生活,绿色出行”是一种环保,健康的生活方式,小丽从甲地出发沿一条笔直的公路骑车前往乙地,她与乙地之间的距离y(km)与出发时间之间的函数关系式如图1中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离S(km)与出发时间x(h)之间的函数关系式如图2中折线段CD-DE-EF所示.
(1)小丽和小明骑车的速度各是多少?
(2)求E点坐标,并解释点的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,∠C=90°,AC=3,BC=4.求作菱形DEFG,使点D在边AC上,点E、F在边AB上,点G在边BC上.
中,∠C=90°,AC=3,BC=4.求作菱形DEFG,使点D在边AC上,点E、F在边AB上,点G在边BC上.
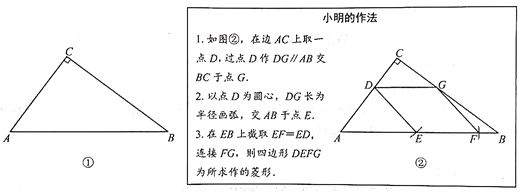
(1)证明小明所作的四边形DEFG是菱形;
(2)小明进一步探索,发现可作出的菱形的个数随着点D的位置变化而变化……请你继续探索,直接写出菱形的个数及对应的CD的长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
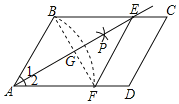
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A′B′C′关于点P成中心对称,则点A′的坐标为( )

A. (﹣4,﹣5) B. (﹣5,﹣4) C. (﹣3,﹣4) D. (﹣4,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
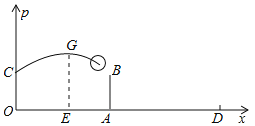
【题目】为如图,已知女排球场的长度OD为18米,位于球场中线处的球网AB的高度2.24米,一队员站在点O处发球,排球从点O的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为6米时,到达最高点G,以O为原点建立如图所示的平面直角坐标系.
(1)若排球运行的最大高度为2.8米,求排球飞行的高度p(单位:米)与水平距离x(单位:米)之间的函数关系式(不要求写自变量x的取值范围);
(2)在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由;
(3)若李明同学发球要想过网,又使排球不会出界(排球压线属于没出界)求二次函数中二次项系数的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com