
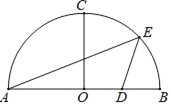
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ�����뾶OC��AB��OB��4��D��OB���е㣬��E�ǻ�BC�ϵĶ��㣬����AE�� DE��
��1������E�ǻ�BC���е�ʱ������ADE�������
��2����tan��AED��![]() ����AE�ij���
����AE�ij���
��3����F�ǰ뾶OC��һ���㣬���E��ֱ��OC�ľ���Ϊm��
�ٵ���DEF�ǵ���ֱ��������ʱ����m��ֵ��
���ӳ�DF����Բ���ڵ�G������AG����EG��AG��DE��ֱ��д��DE�ij��� ����
���𰸡���1��6![]() ����2��
����2��![]() ��3����
��3����![]() ��
��![]()
��������
��1����Ϊ��E�ǻ�BC���е㣬����OE��BE������45������ֱ�������Σ����á�AEB����Ӱ�������۽������̼��ɣ�
��2�������������Ǻ�����������DF��AE����ֱ�������Σ����ų���ƽ�����ƣ�����AD��AB֮�ȣ���ʾAF���á�AFD�������ɹ�ϵ���̣�
��3���ٷֱ���D��E��FΪֱ�Ƕ˵�������ۣ���K��ȫ�Ⱥ���Ӱ�������۽���������⣮
����Ҫ����֤����BDEΪ���������Σ��ù��ɶ������AG���á�AOG����DEB���DE
�⣺��1����ͼ����EH��AB������OE��EB
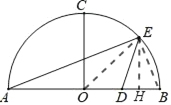
��DH��a����HB��2��a��OH��2+a
�ߵ�E�ǻ�BC�е�
���COE����EOH��45��
��EH��OH��2+a
��Rt��AEB��EH2��AHBH
��2+a��2����6+a����2��a��
���a��![]()
��a��![]() ��
��
S��ADE��![]()
��2����ͼ����DF��AE������ΪF������BE
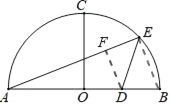
��EF��2x��DF��3x
��DF��BE
��![]()
��![]() ��3
��3
��AF��6x
��Rt��AFD��AF2+DF2��AD2
��6x��2+��3x��2����6��2
���x��![]()
AE��8x��![]() .
.
��3����I.����DΪ����ֱ��������ֱ�Ƕ���ʱ����ͼ
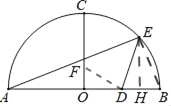
��DH��a
��֤��ODF����EDH
��OD��EH��2
��Rt��ABE��EH2��AHBH
22����6+a����2��a��
���a��![]() ��a=
��a=![]() (����������ȥ)
(����������ȥ)
��DH=![]() �� m��OH =
�� m��OH =![]()
II.����EΪ����ֱ��������ֱ�Ƕ���ʱ����ͼ
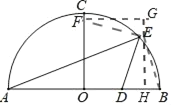
��֤��EFG�ա�EDH
��DH��a����GE��a��EH��CG��2+a
��Rt��ABE��EH2��AHBH
��2+a��2����6+a����2��a��
���a��![]() ��a=
��a=![]() (����������ȥ)
(����������ȥ)
��DH=![]() �� m��OH =
�� m��OH =![]()
III.����FΪ����ֱ��������ֱ�Ƕ���ʱ����ͼ
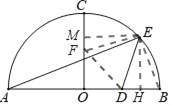
��֤��EFM�ա�ODF
��OF��a����ME��a��MF��OD��2
��EH��a+2��
��Rt��ABE��EH2��AHBH��
��a+2��2����4+a����4��a����
���a��![]() ��a=
��a=![]() ������������ȥ����
������������ȥ����
m��![]() ��
��
����������m��ֵΪ![]() ��
��![]() ��
��![]() .
.
����֤��BDEΪ���������Σ�
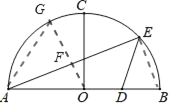
BD��BE��2��
����AOF����ABE��
��OF��1��
��Rt��OFA�У��ɹ��ɶ����ɵ�AF��![]() ��
��
GF��3��
���ɶ����ɵ�AG��![]() ��
��
����AOG����DEB
��![]() ��
��
��DE��![]()


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ж�һ���ͳ������۵ļס��ҡ���3�ִ�����������⣮��������200��������������ΪA��B�����ȼ���A������B��������Ӧ���ݵ�ͳ��ͼ���£�

����������Ϣ������������⣺
��1��a=�� ����b=�� ����
��2����֪�ó����������ִ���750�������ݼ������������Ƹó������ִ������ж��ٴ�B�����ף�
��3�����ڸó��еļ��ֺͱ��ִ��ף����ѡ������һ�֣�����ͳ��֪ʶ�������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y��ax2+bx+c��a��0����ͼ����ͼ��ʾ���Գ���Ϊֱ��x��1��������4�����ۣ���abc��0����4a+2b+c��0����2c��3b����a+b��m��am+b����m�Dz�����1��ʵ������������ȷ�Ľ��۸����У�������

A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�κ���![]() �ͷ���������
�ͷ���������![]() ��ͼ�����㣨1��1����1�����������Ľ���ʽ.��2����֪��
��ͼ�����㣨1��1����1�����������Ľ���ʽ.��2����֪��![]() �ڵ������ޣ���ͬʱ������������ͼ���ϣ����
�ڵ������ޣ���ͬʱ������������ͼ���ϣ����![]() ������.��3�����ã�2���Ľ��������
������.��3�����ã�2���Ľ��������![]() ������Ϊ��2��0�������Ե�
������Ϊ��2��0�������Ե�![]() ,
,![]() ,
,![]() ,
,![]() Ϊ������ı�����ƽ���ı��Σ�����ֱ��д����
Ϊ������ı�����ƽ���ı��Σ�����ֱ��д����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ͥ2018��ÿ�½�ͨ��֧��������ͳ��ͼ�����ü�ͥ2018���½�ͨ��ƽ��֧��ΪaԪ�������н�������ȷ���ǣ�������
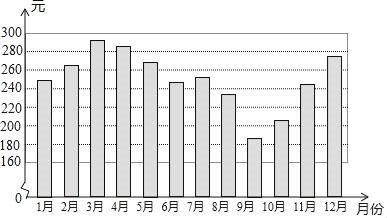
A. 200��a��220B. 220��a��240C. 240��a��260D. 260��a��280
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ۿ���ij���л���Ϊ���˽���У�������Ķ���ѧ�̿������״�������ȡijУ���ֳ���ѧ�����е��飮�������е������ݻ��Ƴ����²�������ͳ��ͼ���������ͼ���е���Ϣ����������⣺
��� | ���� | ռ�������ı��� |
���� | a | 0.3 |
һ�� | 57 | 0.38 |
������ | b | c |
˵����� | 9 | 0.06 |

(1)������������������a��b��c��ֵ������ȫͳ��ͼ��
(2)�ٸ��������ͳ�ƽ����̸̸��Ը�У�������Ķ���ѧ�̿������״�Ŀ��������飻
�����Ҫ�˽�ȫʡ�������Ķ���ѧ�̿�������������ΪӦ����ν��г�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
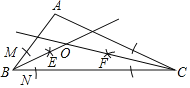
����Ŀ����ͼ���ڡ�ABC�У������²�����ͼ��
����BΪԲ�ģ����ⳤΪ�뾶�������ֱ�AB��BC�ڵ�M��N�����ֱ���M��NΪԲ�ģ��Դ���![]() MN�ij�Ϊ�뾶�����������ཻ�ڵ�E����������BE������ͬ���ķ���������CF��BE��CF�ڵ�O��
MN�ij�Ϊ�뾶�����������ཻ�ڵ�E����������BE������ͬ���ķ���������CF��BE��CF�ڵ�O��
�������ͼ�ش��������⣺
��1��O�ǡ�ABC���� ��
A������ B������ C������
��2����AB��5��AC��12��BC��13����O��BC�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
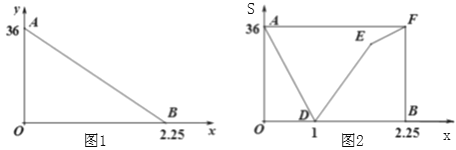
����Ŀ������̼�����ɫ��������һ�ֻ��������������ʽ��С���Ӽس�����һ����ֱ�Ĺ�·�ﳵǰ���ҵأ������ҵ�֮��ľ���y(km)�����ʱ��֮��ĺ�����ϵʽ��ͼ1���߶�AB��ʾ����С��������ͬʱ��С�����ҵ���ͬһ����·�ﳵ����ǰ���أ�����֮��ľ���S(km)�����ʱ��x(h)֮��ĺ�����ϵʽ��ͼ2�����߶�CD-DE-EF��ʾ.
��1��С����С���ﳵ���ٶȸ��Ƕ��٣�
��2����E�����꣬�����͵��ʵ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
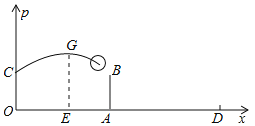
����Ŀ��Ϊ��ͼ����֪Ů���ij���ODΪ18�ף�λ�������ߴ�������AB�ĸ߶�2.24�ף�һ��Ավ�ڵ�O����������ӵ�O�����Ϸ�2��C������ǰ����ȥ������ķ���·���������ߵ�һ���֣����������������O��ˮƽ����OEΪ6��ʱ��������ߵ�G����OΪԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ��
��1�����������е����߶�Ϊ2.8�ף���������еĸ߶�p����λ���ף���ˮƽ����x����λ���ף�֮��ĺ�����ϵʽ����Ҫ��д�Ա���x��ȡֵ��Χ����
��2���ڣ�1���������£�������������ܹ�����������ܹ��������Ƿ����磿��˵�����ɣ�
��3��������ͬѧ����Ҫ���������ʹ������磨����ѹ������û���磩����κ����ж�����ϵ�������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com