
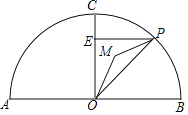
【题目】如图,AB为⊙O的直径,且AO=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM
(1)求∠OMP的度数;
(2)随着点P在半圆上位置的改变,∠CMO的大小是否改变,说明理由;
(3)当点P在半圆上从点B运动到点A时,直接写出内心M所经过的路径长.
【答案】(1)135°;(2)∠CMO的大小不改变,理由见解析;(3)![]() .
.
【解析】
(1)由内心的定义可知∠MOP=∠MOC=![]() ∠EOP,∠MPO=∠MPE=
∠EOP,∠MPO=∠MPE=![]() ∠EPO,求出∠MOP与∠MPO的和为45°,利用三角形的内角和定理即可求出∠OMP的度数;
∠EPO,求出∠MOP与∠MPO的和为45°,利用三角形的内角和定理即可求出∠OMP的度数;
(2)连接CM,证△COM≌△POM,即得出∠CMO=∠OMP=135°,可知∠CMO的大小不改变,为135°;
(3)连接AC,BC,证明△ACB,△ACO与△BCO为分别为等腰直角三角形,求出CQ=2![]() ,∠CQO=90°,∠CNO=90°,由题意分析得出当点P在半径OC的左侧和右侧的半圆上时,点M的轨迹分别在以AC,BC为直径的圆弧上,根据弧长公式即可求出M所经过的路径长.
,∠CQO=90°,∠CNO=90°,由题意分析得出当点P在半径OC的左侧和右侧的半圆上时,点M的轨迹分别在以AC,BC为直径的圆弧上,根据弧长公式即可求出M所经过的路径长.
解:(1)∵OC⊥AB,
∴∠OEP=90°,
∴∠EOP+∠EPO=90°,
∵M为△OPE的内心,
∴∠MOP=∠MOC=![]() EOP,∠MPO=∠MPE=
EOP,∠MPO=∠MPE=![]() ∠EPO,
∠EPO,
∴∠MOP+∠MPO=![]() (∠EOP+∠EPO)=45°,
(∠EOP+∠EPO)=45°,
∴∠OMP=180°﹣(∠MOP+∠MPO)=135°;
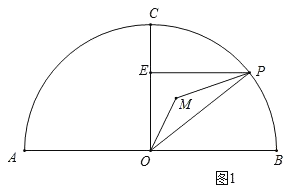
(2)∠CMO的大小不改变,理由如下:
如图2,连接CM,
在△COM和△POM中,
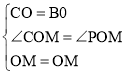 ,
,
∴△COM≌△POM(SAS),
∴∠CMO=∠OMP=135°,
∴∠CMO的大小不改变,为135°;
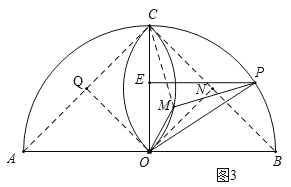
(3)如图3,连接AC,BC,
∵AB为直径,CO⊥AB,
∴AC=BC,
∴△ACB为等腰直角三角形,
∴△ACO与△BCO为等腰直角三角形,
∴AC=![]() ,
,
∴CQ=![]()
分别取AC,BC的中点Q,N,连接OQ,ON,
则∠CQO=90°,∠CNO=90°,
当点P在半径OC的左侧和右侧的半圆上时,点M的轨迹分别在以AC,BC为直径的圆弧上,所对圆心角为90°,
∴![]() ,
,
∴内心M所经过的路径长为2![]()



 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
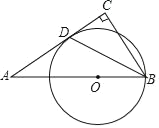
【题目】如图,∠BCA=90°,点O在△ABC的斜边AB上,以OB为半径的⊙O经过点B,与AC相切于点D,连结BD.
(1)求证;BD平分∠ABC;
(2)若∠ABC=60°,OB=2,计算△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代算书《九章算术》中第九章第六题是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深葭长各几何?你读懂题意了吗?请回答水深______尺,葭长_____尺.解:根据题意,设水深OB=x尺,则葭长OA'=(x+1)尺.可列方程正确的是( )
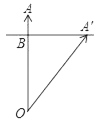
A. x2+52 =(x+1)2B. x2+52 =(x﹣1)2
C. x2+(x+1)2 =102D. x2+(x﹣1)2=52
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |
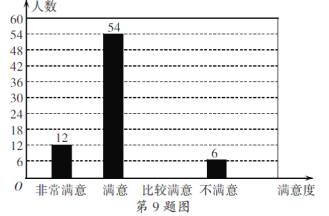
根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 为了解全省中学生的心理健康状况,宜采用普查方式
B. 掷两枚质地均匀的硬币,两枚硬币都是正面朝上这一事件发生的概率为![]()
C. 掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
D. 甲乙两人在相同条件下各射击10次,他们成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )

A. (3,4)或(2,4) B. (2,4)或(8,4)
C. (3,4)或(8,4) D. (3,4)或(2,4)或(8,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的动点,PC∥AB,点M是OP中点.
(1)求证:四边形OBCP是平行四边形;
(2)填空:
①当∠BOP= 时,四边形AOCP是菱形;
②连接BP,当∠ABP= 时,PC是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的 日销售量(件)与时间(天)的关系如下表:
时间(天) | 1 | 3 | 6 | 10 | 36 | … |
日销售量(件) | 94 | 90 | 84 | 76 | 24 | … |
未来40天内,前20天每天的价格y1(元/件)与t时间(天)的函数关系式为:y1=![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—
t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—![]() t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
(1)认真分析上表中的数量关系,利用学过的一次函数、二次函数 、反比例函数的知识确定一个满足这些数据之间的函数关系式;
(2)请预测未来40天中那一天的销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程,公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com