
����Ŀ���������֣�
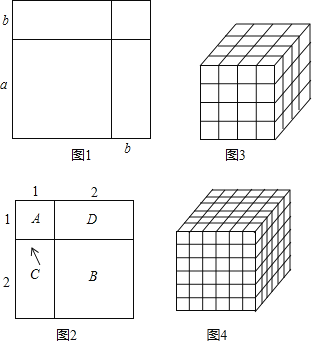
���ν���ǽ����ѧ�����һ����Ҫ��˼�뷽�����������ַ����ɽ��������ѧ֪ʶ���ֱ���������Ҿ��пɲ����ԣ��Ӷ����������ǿ��ٽ��⣮������ѧ���һЩ������ʽ���ܶ����ͨ����ʾ����ͼ������ķ�������ֱ���Ƶ��ͽ��ͣ����磺����ͼ�εļ���������֤��ȫƽ����ʽ����һ���߳�Ϊa�������εı߳�����b���γ��������κ����������Σ���ͼ1�����ͼ�ε�������Ա�ʾ�ɣ���a+b��2��a2+2ab+b2�ࣨa+b��2��a2+2ab+b2
�����֤�������͵���ȫƽ����ʽ��
���������
�������ͼ�μ�������ķ�����֤��13+23��32 ��ͼ2��A��ʾ1��1��1�������Σ�����1��1��1��13��B��ʾ1��2��2�������Σ�C��Dǡ�ÿ���ƴ��1��2��2�������Σ���ˣ�B��C��D�Ϳ��Ա�ʾ2��2��2�������Σ�����2��2��2��23����A��B��C��Dǡ�ÿ���ƴ��һ����1+2������1+2���Ĵ������Σ��ɴ˿ɵã�13+23����1+2��2��32
���Խ����
������������Ƶ����̣�����ͼ�μ������巽����֤��13+23+33���� ����Ҫ���Լ�����ͼ�β�д����֤���̣�
��ȹ��ɣ�
��������ı�ʾ����ͼ������ķ���̽����13+23+33+��+n3���� ����Ҫ��ֱ��д�����ۣ�����д��������̣�
ʵ��Ӧ�ã�
ͼ3�����ⳤΪ1��С�������ɵĴ������壬ͼ�д�С������һ���ж��ٸ���Ϊ����ȷ������С��������ܸ��������ǿ��Է���ͳ�ƣ����ֱ������ⳤ��1��2��3��4��������ĸ����������ܺͣ�
���磺�ⳤ��1���������У�4��4��4��43�����ⳤ��2���������У�3��3��3��33�����ⳤ��3���������У�2��2��2��23�����ⳤ��4���������У�1��1��l��13����Ȼ�����ã�3����ȹ��ɵĽ��ۣ��ɵã��������� ��ͼ4�����ⳤΪ1��С������ɵĴ������壬ͼ�д�С������һ������ ������
����Ӧ�ã�
������ⳤΪ1��С�������ɵĴ��������У�ͨ������ķ�ʽ�����Ĵ�С������һ����44100������ô�ⳤΪ1��С������һ������ ������
���𰸡���1����1+2+3��2����2����1+2+3+��+n��2����3��13+23+33+43����1+2+3+4��2��100������4��8000��
��������
���ݹ��ɿ���������ͬ�ķ�������̽����֤��������̽��13+23+33�����϶����ɴ���������9������ͼ�Σ�3��������6�������Σ���ɣ���ͼ��ʾ������֤��
ʵ��Ӧ�ã����ݹ�������������к��ж��ٸ������壬����ת��Ϊ13+23+33+��+n3����1+2+3+��+n��2����ã�
����Ӧ�ã��ɽ��ܸ�������m2��Ȼ����д�ɣ���1+2+3+��+n��2�ó���������ÿ�������м����ⳤΪ1��С�����壬����������ⳤΪ1��С������ĸ�����
�⣺��ͼ��A��ʾ1��1��1�������Σ���1��1��1��13��
B��ʾ1��2��2�������Σ�C��Dǡ�ÿ���ƴ��1��2��2�������Σ�
���B��C��D�Ϳ���ƴ��2��2��2�������Σ�����2��2��2��23��
G��H��E��F�Ϳ���ƴ��3��3��3�������Σ�����3��3��3��33��
������ͼ��ǡ�ÿ���ƴ��һ����1+2+3������1+2+3���Ĵ������Σ�
��˿ɵã�13+23+33����1+2+3��2��62��
�ʴ�Ϊ����1+2+3��2��62��
���ݹ��ɿɵã�13+23+33+��+n3����1+2+3+��+n��2��
���ݹ��ɵã�13+23+33+43����1+2+3+4��2��102��100��
�ʴ�Ϊ��13+23+33+43����1+2+3+4��2 100
��44100��2102����1+2+3+��+n��2
��n��20
��20��20��20��8000
�ʴ�Ϊ8000��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η��̣�m+1��x2+2��m+1��x+2��0��������ȵ�ʵ������������y����x2+��m+1��x+3��x�ύ��A��B���㣨A��B��ࣩ����y���ཻ�ڵ�C�������ߵĶ���ΪD��
��1���������ߵĽ���ʽ��
��2����ͼ1���������ߵĶ��ύx���ڵ�E���������ߵĶԳ������Ƿ���ڵ�P��ʹP�㵽x��ľ������P�㵽ֱ��BD�ľ��룿�����ڣ������P�����꣬�������ڣ���˵�����ɣ�
��3����ͼ2����CF��DE��F��MΪ����EA��һ���㣮������߶�EF��ǡ�ô���������N������CFN����NEM���ƣ���M������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���![]() �У�BC=3������
��BC=3������![]() ��
��![]() ��������ÿ��1����λ���ٶȣ�������
��������ÿ��1����λ���ٶȣ�������![]() �����ƶ�����
�����ƶ�����![]() ����ֱ��
����ֱ��![]() �ĶԳ�
�ĶԳ�![]() �����
�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]()
��1����![]()
����ͼ2������B������AC��ʱ����Ȼ��PCB����ֱ�������Σ����ʱt��ֵ
���Ƿ��������ͼ2��ʱ�̣�ʹ����PCB����ֱ�������Σ������ڣ���ֱ��д�����з��������t��ֵ���������ڣ���˵������
��2����P�㲻��C���غ�ʱ����ֱ��PB����ֱ��CD�ཻ�ڵ�M���ҵ�t��3ʱ����ijһʱ���н��ۡ�PAM=45����������̽��������t��3������ʱ�̣����ۡ�PAM=45���Ƿ����dz�������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���˼����
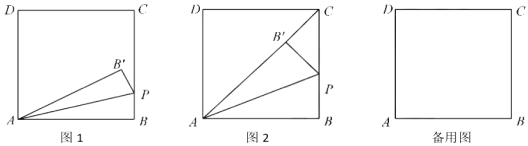
�����£���Ԫǰ287��һ��Ԫǰ212�꣩��ΰ��Ĺ�ϣ����ѧ�ҡ��ٿ�ʽ��ѧ�ҡ���ѧ�ҡ�����ѧ�ҡ���ѧ�ң���̬��ѧ�����徲��ѧ�ĵ���ˣ�����������������������10���֣���Ϊϣ�����ָ������ǡ�������ȫ�����м��ص�һ�����⣺AB����O���ң���C����O�ϣ���CD��AB�ڵ�D������AB��ȡ��E��ʹAD��DE����F��![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ��
��![]() ������BF�ɵ�BF��BE��
������BF�ɵ�BF��BE��
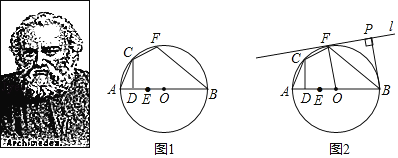
��1����������������AB��Ϊֱ��AB����ͼ1��ʾ����֤��BF��BE��
��2����ͼ2��ʾ����ֱ��AB��10��EO��![]() OB����ֱ��l����O�����ڵ�F������B��BP��l�ڵ�P����BP�ij���
OB����ֱ��l����O�����ڵ�F������B��BP��l�ڵ�P����BP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��ο��ṩ���õķ���ij��������Բ����οͽ����˹��ڡ���������������ȡ��ĵ��飬�����ݵ��������Ƴ����²�������ͳ��ͼ��.
����� | ���� | ��ռ�ٷֱ� |
�dz����� | 12 | 10% |
���� | 54 | m |
�Ƚ����� | n | 40% |
������ | 6 | 5% |
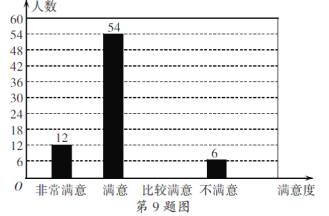
����ͼ����Ϣ������������⣺
(1)���ε����������Ϊ______������m��ֵΪ_______��
(2)�벹ȫ����ͳ��ͼ��
(3)��ͳ�ƣ��þ���ƽ��ÿ��Ӵ��ο�Լ3600�ˣ��������dz����⡱�͡����⡱��Ϊ�οͶԾ����������Ŀ϶���������Ƹþ���������ƽ��ÿ��õ��������ο͵Ŀ϶�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
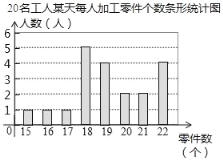
����Ŀ��ij����Ϊ�˽�˵�������������������˳������飮�ò��������ȡ��20������ij��ÿ�˼ӹ�����ĸ������������£������������ݣ��õ�����ͳ��ͼ���������ݵ�ƽ��������������λ�������ʾ��
ͳ���� | ƽ���� | ���� | ��λ�� |
��ֵ | 19.2 | m | n |
����������Ϣ������������⣺
��1���ϱ���m��n��ֵ�ֱ�Ϊ�� ������ ����
��2��Ϊ���������ԣ��ò��Ÿ��ݹ���ÿ��ӹ�����ĸ����ƶ��˽���������������������Ĺ��˽���ý������������60%���ҵĹ����ܻ�Ӧ������ ����ȷ���������ȽϺ��ʣ�����ƽ����������������������λ��������
��3���ò��Ź涨��ÿ��ӹ�����ĸ����ﵽ��21���Ĺ���Ϊ�����������ò�����300�����ˣ��Թ��Ƹò����������ֵ�������
��4���־�����С����С�š�С�С����ѡ���˲μ�ҵ�����ֱ�����ֱ��д��ǡ��ѡ��С�š�С�����˵ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2����2m+3��x+m2+2��0��
��1����������ʵ��������ʵ��m��ȡֵ��Χ��
��2����������ʵ�����ֱ�Ϊx1��x2��������x12+x22��31+|x1x2|����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʻС�������ٵش�A����ʹ��B�أ���ʻ���Ϊ480ǧ�ף���С��������ʹʱ��Ϊt����λ��Сʱ������ʹ�ٶ�Ϊv����λ��ǧ��/Сʱ������ȫ���ٶ���Ϊ������120ǧ��/Сʱ.
����v����t�ĺ�������ʽ��
�Ʒ�������8���ʻС������A����.
�ٷ������ڵ���12��48����14�㣨��12��48�ֺ�14�㣩�䵽��B�أ���С������ʻ�ٶ�v�ķ�Χ.
�ڷ����ܷ��ڵ���11��30��ǰ����B�أ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ����,��ͼ,����ABCD��,AB=10��AD=15��![]() ����PΪAD���������,����PB����PB�Ƶ�P��ʱ����ת90��õ��߶�PQ.
����PΪAD���������,����PB����PB�Ƶ�P��ʱ����ת90��õ��߶�PQ.
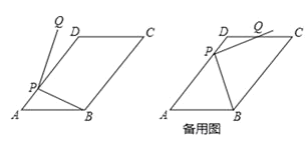
��1������DPQ= 10��ʱ������APB�Ĵ�С��
��2���� ![]() ʱ,���Q���B��ľ���(�����������)��
ʱ,���Q���B��ľ���(�����������)��
��3������Qǡ�����ڿ�ABCD�ı����ڵ�ֱ����,ֱ��д��PB��ת��PQ��ɨ�������.(���������).
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com