
【题目】平面内,如图,在□ABCD中,AB=10,AD=15,![]() ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
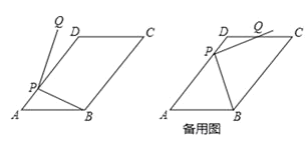
(1)当∠DPQ= 10°时,求∠APB的大小;
(2)当 ![]() 时,求点Q与点B间的距离(结果保留根号);
时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在口ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π).
【答案】(1)当∠DPQ=10°时,∠APB的值为80°或100°;(2)![]() ;(3)PB旋转到PQ所扫过的面积为32π或20π或16π.
;(3)PB旋转到PQ所扫过的面积为32π或20π或16π.
【解析】
(1)根据题意画出图形分情况讨论:①当点Q在平行四边形ABCD内时,②当点Q在平行四边形ABCD外时,结合题意分别求得答案.
(2) 连接BQ,作PE⊥AB于E,由已知结合题意即可求得tan∠ABP=2,在Rt△APE中,根据正切函数定义可设PE=4k,则AE=3k,在Rt△PBE中,根据正切函数定义可得EB=2k,
由AB=AE+EB即可求得k值,从而可得PE=8,EB=4,在Rt△PBE中,根据勾股定理可求得PB长,由等腰直角三角形性质可求得BQ长 .
(3)分三种情形分别求解即可; ①如图,当点Q落在直线BC上时,作BE⊥AD于E,PF⊥BC于F;在Rt△AEB中,根据正切tanA的值可求得BE=8,AE=6,从而可得PF=BE=8,根据等腰直角三角形的性质可得PF=BF=FQ=8,根据勾股定理可得PB=PQ=![]() ,根据扇形面积公式可得PB旋转到PQ所扫过的面积;
,根据扇形面积公式可得PB旋转到PQ所扫过的面积;
②如图,当点Q落在CD上时,作BE⊥AD于E,QF⊥AD交AD的延长线于F;设PE=x,由全等三角形判定可得△PBE≌△QPF,再由正切函数定义列方程可求PE=4,在Rt△PEB中,根据勾股定理求得PB=4![]() ,根据扇形面积公式可得PB旋转到PQ所扫过的面积;
,根据扇形面积公式可得PB旋转到PQ所扫过的面积;
③如图,当点Q落在AD上时,易知PB=PQ=8,根据扇形面积公式可得PB旋转到PQ所扫过的面积.
(1)解:如图1中,
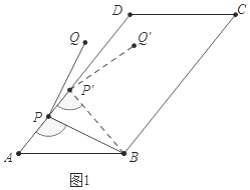
①当点Q在平行四边形ABCD内时,∠AP′B=180°∠Q′P′B∠Q′P′D=180°90°10°=80°
②当点Q在平行四边形ABCD外时,∠APB=180°(∠QPB∠QPD)=180°(90°10°)=100°
综上所述,当∠DPQ=10°时,∠APB的值为80°或100°
(2)如图2中,连接BQ,作PE⊥AB于E.
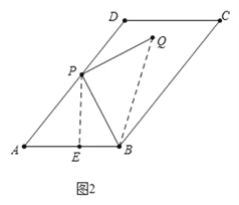
∵tan∠ABP:tanA=3:2,tanA=![]() ,
,
∴tan∠ABP=2,在Rt△APE中,tanA=![]() ,
,
设PE=4k,则AE=3k,在Rt△PBE中,tan∠ABP=![]() =2,
=2,
∴EB=2k,
∴AB=5k=10,
∴k=2,
∴PE=8,EB=4,
∴PB=![]() ,
,
∵△BPQ是等腰直角三角形,
∴BQ=![]() PB=
PB= ![]() .
.
(3)①如图3中,当点Q落在直线BC上时,作BE⊥AD于E,PF⊥BC于F. 则四边形BEPF是矩形。
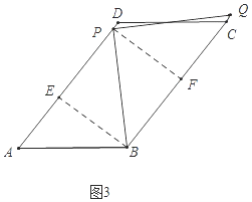
在Rt△AEB中,∵tanA=![]() ,
,
∵AB=10,∴BE=8,AE=6,
∴PF=BE=8,
∵△BPQ是等腰直角三角形,PF⊥BQ,∴PF=BF=FQ=8,
∴PB=PQ=![]() ,
,
∴PB旋转到PQ所扫过的面积=![]() .
.
②如图4中,当点Q落在CD上时,作BE⊥AD于E,QF⊥AD交AD的延长线于F. 设PE=x.
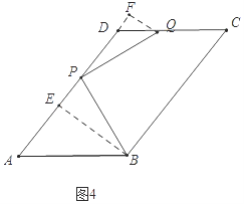
易证△PBE≌△QPF,
∴PE=QF=x,EB=PF=8,∴DF=AE+PE+PFAD=x1,∵CD∥AB,∴∠FDQ=∠A,
∴tan∠FDQ=tanA=![]() ,
,
∴![]() ,
,
∴x=4,∴PE=4,
在Rt△PEB中,PB= ![]() ,
,
∴PB旋转到PQ所扫过的面积=![]() .
.
③如图5中,
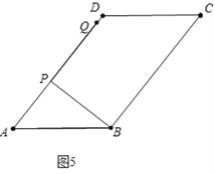
当点Q落在AD上时,易知PB=PQ=8,
∴PB旋转到PQ所扫过的面积=![]() ,
,
综上所述,PB旋转到PQ所扫过的面积为32π或20π或16π.


科目:初中数学 来源: 题型:
【题目】问题再现:
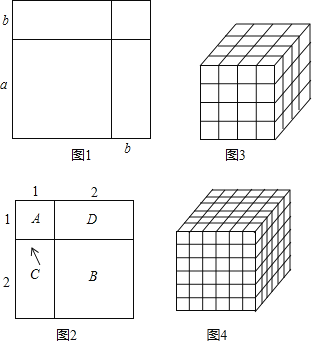
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:利用图形的几何意义推证完全平方公式.将一个边长为a的正方形的边长增加b,形成两个矩形和两个正方形,如图1,这个图形的面积可以表示成:(a+b)2或a2+2ab+b2∴(a+b)2=a2+2ab+b2
这就验证了两数和的完全平方公式.
问题提出:
如何利用图形几何意义的方法推证:13+23=32 如图2,A表示1个1×1的正方形,即:1×1×1=13,B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23,而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形,由此可得:13+23=(1+2)2=32
尝试解决:
请你类比上述推导过程,利用图形几何意义方法推证:13+23+33= (要求自己构造图形并写出推证过程)
类比归纳:
请用上面的表示几何图形面积的方法探究:13+23+33+…+n3= (要求直接写出结论,不必写出解题过程)
实际应用:
图3是由棱长为1的小正方体搭成的大正方体,图中大小正方体一共有多少个?为了正确数出大小正方体的总个数,我们可以分类统计,即分别数出棱长是1,2,3和4的正方体的个数,再求总和.
例如:棱长是1的正方体有:4×4×4=43个,棱长是2的正方体有:3×3×3=33个,棱长是3的正方体有:2×2×2=23个,棱长是4的正方体有:1×1×l=13个,然后利用(3)类比归纳的结论,可得: = 图4是由棱长为1的小正方体成的大正方体,图中大小正方体一共有 个.
逆向应用:
如果由棱长为1的小正方体搭成的大正方体中,通过上面的方式数出的大小正方体一共有44100个,那么棱长为1的小正方体一共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
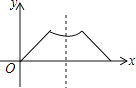
A. 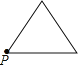 B.
B. 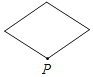 C.
C. 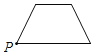 D.
D. 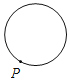
查看答案和解析>>
科目:初中数学 来源: 题型:
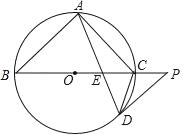
【题目】如图,已知BC是⊙O的直径,点A,D在⊙O上,∠B=2∠CAD,在BC的延长线上有一点P,使得∠P=∠ACB,弦AD交直径BC于点E.
(1)求证:DP与⊙O相切;
(2)判断△DCE的形状,并证明你的结论;
(3)若CE=2,DE=![]() ,求线段BC的长度.
,求线段BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行了1000米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图.
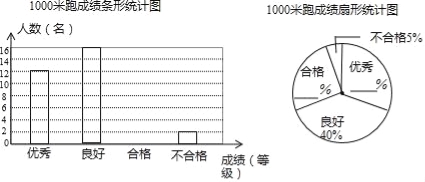
(1)根据给出的信息,补全两幅统计图;
(2)该校九年级有600名男生,请估计成绩未达到良好有多少名?
(3)某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛,预赛分为A、B、C三组进行,选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
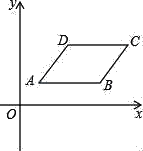
【题目】如图,在平面直角坐标系中,ABCD的边AB=2,顶点A坐标为(1,b),点D坐标为(2,b+1)
(1)点B的坐标是 ,点C的坐标是 (用b表示);
(2)若双曲线y=![]() 过ABCD的顶点B和D,求该双曲线的表达式;
过ABCD的顶点B和D,求该双曲线的表达式;
(3)若ABCD与双曲线y=![]() (x>0)总有公共点,求b的取值范围.
(x>0)总有公共点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
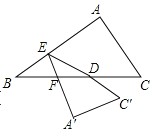
【题目】如图,在Rt△ABC中,AC=3,AB=4,D为斜边BC的中点,E为AB上一个动点,将△ABC沿直线DE折叠,A,C的对应点分别为![]() ,
,![]() ,
,![]() 交BC于点F,若△BEF为直角三角形,则BE的长度为______.
交BC于点F,若△BEF为直角三角形,则BE的长度为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com