
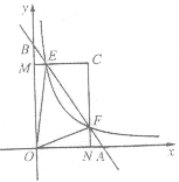
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若![]() (
(![]() 为大于l的常数).记△CEF的面积为
为大于l的常数).记△CEF的面积为![]() ,△OEF的面积为
,△OEF的面积为![]() ,则
,则![]() =________. (用含
=________. (用含![]() 的代数式表示)
的代数式表示)
【答案】![]() (k的几何意义,线段比的转化,面积的几种求法)
(k的几何意义,线段比的转化,面积的几种求法)
【解析】过点F作FD⊥BO于点D,EW⊥AO于点W,
∵BE/BF =1/m ,∴FN/EW =1/m ,
设E点坐标为:(x,my),则F点坐标为:(mx,y),
∴△CEF的面积为:S1= ![]() (mx-x)(my-y)=
(mx-x)(my-y)= ![]() (m-1)2xy,
(m-1)2xy,
∵△OEF的面积为:S2=S矩形CNOM-S1-S△MEO-S△FON,
=MCCN- ![]() (m-1)2xy-
(m-1)2xy- ![]() MEMO-
MEMO- ![]() FNNO,
FNNO,
=mxmy- ![]() (m-1)2xy-
(m-1)2xy- ![]() xmy-
xmy- ![]() ymx,
ymx,
=m2xy- ![]() (m-1)2xy-mxy,
(m-1)2xy-mxy,
= ![]() (m2-1)xy,
(m2-1)xy,
= ![]() (m+1)(m-1)xy,
(m+1)(m-1)xy,
∴S1/S2 = 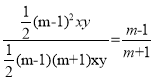 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
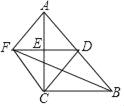
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是BC上任意一点,将线段AD绕点A逆时针方向旋转
,点D是BC上任意一点,将线段AD绕点A逆时针方向旋转![]() ,得到线段AE,连结EC.
,得到线段AE,连结EC.
![]() 依题意补全图形;
依题意补全图形;
![]() 求
求![]() 的度数;
的度数;
![]() 若
若![]() ,
,![]() ,将射线DA绕点D顺时针旋转
,将射线DA绕点D顺时针旋转![]() 交EC的延长线于点F,请写出求AF长的思路.
交EC的延长线于点F,请写出求AF长的思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
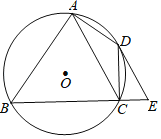
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
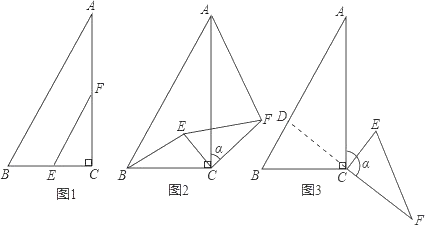
【题目】如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
(1)线段BE与AF的位置关系是 ,![]() = .
= .
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6﹣2![]() ,求旋转角a的度数.
,求旋转角a的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别是边AB、AC的中点,延长DE至F,使得AF∥CD,连接BF、CF.
(1)求证:四边形AFCD是菱形;
(2)当AC=4,BC=3时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
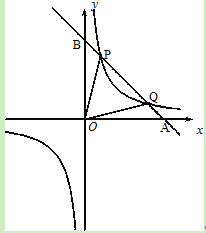
【题目】
如图,已知反比例函数![]() 的图象经过点(
的图象经过点(![]() ,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
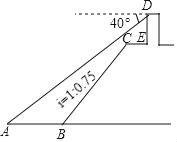
【题目】如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号):
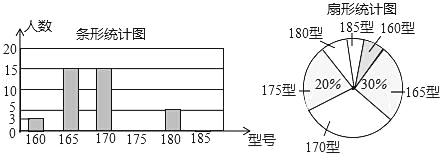
根据以上信息,解答下列问题:
(1)该班共有 名学生;
(2)补全条形统计图;
(3)该班学生所穿校服型号的众数为 ,中位数为 ;
(4)如果该校预计招收新生1500名,根据样本数据,估计新生穿170型校服的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
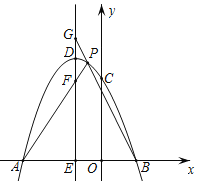
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,与y轴交于C(0,3),抛物线的顶点坐标为D(﹣1,4).
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P不与B、D两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com