
【题目】
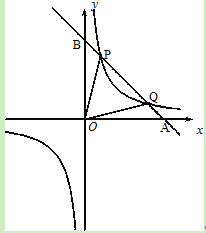
如图,已知反比例函数![]() 的图象经过点(
的图象经过点(![]() ,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积.
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
【题目】如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=![]() 的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.
的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx+c的图象交于点(4,﹣3),(﹣1,12).
(1)求二次函数的解析式;
(2)二次函数与x轴交于点A,B,与y轴交于点C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=3,AD=8,点E为BC的中点,连接AE,EF是∠AEC的平分线,交AD于点F,则FD=( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
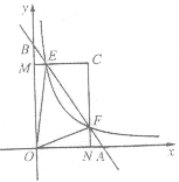
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若![]() (
(![]() 为大于l的常数).记△CEF的面积为
为大于l的常数).记△CEF的面积为![]() ,△OEF的面积为
,△OEF的面积为![]() ,则
,则![]() =________. (用含
=________. (用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
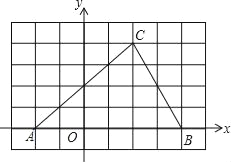
【题目】如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
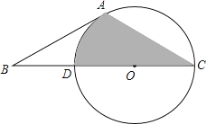
【题目】如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(1)求证:AB为⊙O的切线;
(2)求弦AC的长;
(3)求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2015年投入教育经费2900万元,2017年投入教育经费3509万元.
(1)求2015年至2017年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的增长情况,该地区到2019年需投入教育经费4250万元,如果按(1)中教育经费投入的增长率,到2019年该地区投入的教育经费是否能达到4250万元?请说明理由.
(参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com