
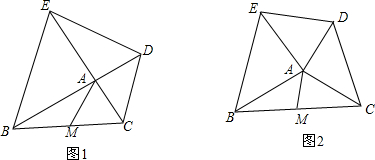
���� ��1����ֱ��������б�������ߵ����ʿ�֪AM=$\frac{1}{2}$CB��Ȼ����֤����ABC�ա�AED���Ӷ���֤��BC=DE����֤�ã�AM=$\frac{1}{2}$DE���ɡ�BAC�ա�DAE��Ȼ����֤����AEN+��EAN=90�㣬��֪AM��DE��
��2���ӳ�AM��K��ʹMK=AM������BK��CK����֤���ı���ABKC��ƽ���ı��Σ�Ȼ����֤����ABK�ա�EAD��SAS�����Ӷ���֤�ã�DE=2AM���ٸ��ݡ�AED+��EAN=��BAK+��EAN=180��-90��=90�㣬��֤��AM��DE��
��3���ӳ�AM��P��ʹMP=MA������BP����BM=CM����BMP=��CMA��֤�á�BMP�ա�CMA��SAS�����Ӷ��õ���BP=AC=AD����BPM=��CAM��Ȼ���ɡ�BAE+��CAD=��+��180��-����=180�㣬��֪��ABP=��EAD����֤�á�ABP�ա�EAD��SAS���Ӷ���֤��DE=2AM���ɡ�AND=��CAD�������ж�AM��DE��һ����ֱ��
��� �⣺��1�����ۣ�DE=2AM��AM��DE��
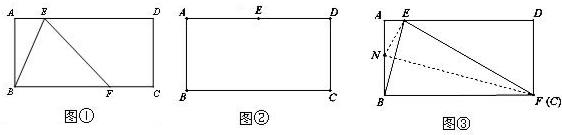
���ɣ���ͼ1�У��ӳ�MA��DE��N��
��M��BC���е㣬��BAC=90�㣬
��AM=$\frac{1}{2}$BC��AM=MC��
�ڡ�BAC�͡�DAE��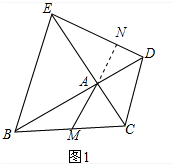 ��
��
$\left\{\begin{array}{l}{AB=AE}\\{��BAC=��EAD}\\{AC=AD}\end{array}\right.$��
���BAC�ա�DAE��
��BC=DE��
��AM=$\frac{1}{2}$DE��
��AM=MC��
���MCA=��MAC��
�ߡ�CBA+BCA=90�㣬
���CBA+��MAC=90�㣬
�ߡ�BAC�ա�DAE��
���CBA=��AED��
�֡ߡ�MAC=��NAE��
���AEN+��EAN=90�㣬
��AM��DE��
��2����1���н��۳�����
���ɣ���ͼ2���ӳ�AM��K��ʹMK=AM������BK��CK��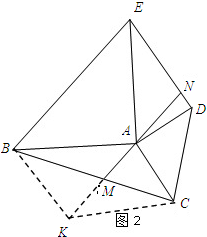 ��MΪBC�ߵ��е㣬
��MΪBC�ߵ��е㣬
��BM=CM��
���ı���ABKC��ƽ���ı��Σ�
��AC=BK=AD����ABK+��BAC=180�㣬
�ߡ�DAC=��EAB=90�㣬
���DAE+��BAC=180�㣬
���ABK=��DAE��
�ڡ�ABK�͡�EAD�У�
$\left\{\begin{array}{l}{BK=AD}\\{��ABK=��DAE}\\{AB=AE}\end{array}\right.$��
���ABK�ա�EAD��SAS����
��AK=DE����BAK=��AED��
��DE=2AM��
�ߡ�AED+��EAN=��BAK+��EAN=180��-90��=90�㣬
��AM��DE��
��DE=2AM��AM��DE��
��3��������ϵ������DE=2AM��λ�ù�ϵ��������
���ɣ���ͼ3���ӳ�AM��P��ʹMP=MA������BP��
�ڡ�BMP�͡�CMA�У�
$\left\{\begin{array}{l}{BM=CM}\\{��BMP=��CMA}\\{MP=MA}\end{array}\right.$��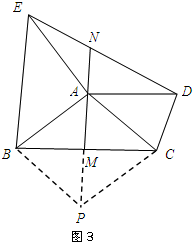
���BMP�ա�CMA��SAS����
��BP=AC=AD����BPM=��CAM��
�֡ߡ�PBM=��ACM��
��BP��AC����ABP+��ABP+��BAC=180�㣬
�֡ߡ�BAE+��CAD=180�㣬
���DAE+��BAC=180�㣬
���ABP=��EAD��
�ڡ�ABP�͡�EAD�У�
$\left\{\begin{array}{l}{BP=AD}\\{��ABP=��EAD}\\{BA=AE}\end{array}\right.$��
���ABP�ա�EAD��SAS����
��PA=DE����BPA=��EDA=��PAC��
��PA=2AM��
��DE=2AM��
�ߡ�PAD=��CAD+��PAC=��AND+��EDA��
���AND=��DAC��
���AND��һ��Ϊ90�㣬
��AM��DE��һ����ֱ��
���� ������Ҫ�������ȫ�������ε����ʺ��ж���ͬʱ����漰��ƽ���ı��Ρ�ֱ��������б���ϵ����ߵ����ʣ����մ�������ĸ����ߵ������ǽ���Ĺؼ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
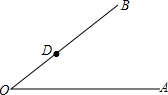 ��֪����ͼ����A0B���ϵĵ�D������D��DF��OA����������ͼ�ۼ�����д���������м��ַ�����
��֪����ͼ����A0B���ϵĵ�D������D��DF��OA����������ͼ�ۼ�����д���������м��ַ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
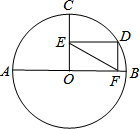 ��ͼ����O��ֱ��AB=4���뾶OC��AB����D�ڻ�BC�ϣ�DE��OC��DF��AB������ֱ�ΪE��F����OE•OF���㣨������
��ͼ����O��ֱ��AB=4���뾶OC��AB����D�ڻ�BC�ϣ�DE��OC��DF��AB������ֱ�ΪE��F����OE•OF���㣨������| A�� | OE•OF��1 | B�� | OE•OF��2 | C�� | OE•OF��3 | D�� | OE•OF��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ����һ | B�� | ���ڶ� | C�� | ������ | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
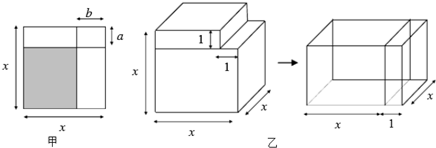
| A�� | $\frac{1}{4}x+1$ | B�� | 4x-1 | C�� | 4��x-1�� | D�� | 4��x+1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com