
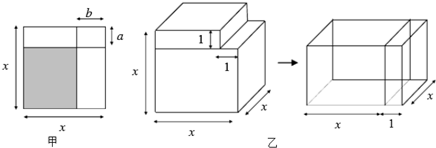
分析 (1)先求得阴影部分矩形的长与宽可直接求得阴影部分的面积,然后依据阴影部分的面积=正方形的面积-1个边长分别为a、x的矩形-1个边长分别为b、x的矩形+一个边长分别为a、b的矩形,从而得到恒等式;
(2)依据(1)的结果可知(a-m)(a-2)=a2-(m+2)a+2m,然后根据两个多项式的对应项相同求解即可;
(3)分别求得图中几何体的体积,然后根据原图形与新图形体积相等列出恒等式即可.
解答 解:(1)①阴影部分的面积=(x-a)(x-b),②阴影部分的面积=x2-ax-bx+ab=x2-(a+b)x+ab,
∵阴影部分的面积不变,
∴(x-a)(x-b)=x2-(a+b)x+ab.
故答案为:①(x-a)(x-b);②x2-(a+b)x+ab;(x-a)(x-b)=x2-(a+b)x+ab.
(2)由(1)可知:(a-m)(a-2)=a2-(m+2)a+2m,
又∵(a-m)(a-2)=a2+na+6,
∴2m=6,n=-(m+2).
解得:m=3,n=-5.
(3)∵原几何体的体积=x3-1×1•x=x3-x,新几何体的体积=(x+1)(x-1)x,
∴x3-x=(x+1)(x-1)x.
点评 本题主要考查的是整式的混合运算,利用直接法和间接法分别求得几何图形的体积或面积,然后根据它们的体积或面积相等列出等式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
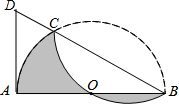 已知,如图,AB是半圆O的直径,点C是$\widehat{AB}$上一点,现将半圆沿BC折叠,$\widehat{BC}$恰好过圆心O,点D为BC延长线上一点,且AD与⊙O相切.
已知,如图,AB是半圆O的直径,点C是$\widehat{AB}$上一点,现将半圆沿BC折叠,$\widehat{BC}$恰好过圆心O,点D为BC延长线上一点,且AD与⊙O相切.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
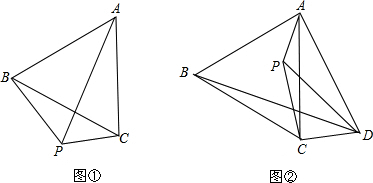
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
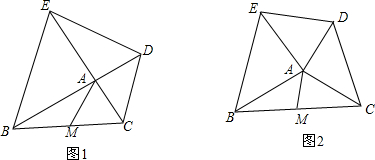
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com