
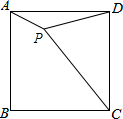
 如图,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,则∠APD的度数为( )
如图,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,则∠APD的度数为( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
分析 将三角形APD绕点D沿逆时针旋转90°到达△CDQ的位置,将分散的条件PA、PD、PC集中到△PQC、△DQC中;证明PC2=PQ2+CQ2,根据勾股定理的逆定理求出∠PQC=90°;然后求出∠PQD=45°,得到∠DQC的度数,即可解决问题.
解答 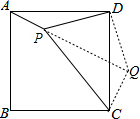 解:如图,将三角形APD绕点D沿逆时针旋转90°到达△CDQ的位置;
解:如图,将三角形APD绕点D沿逆时针旋转90°到达△CDQ的位置;
则∠PDQ=90°,QD=PD=2,QC=AP=1;由勾股定理得:
PQ2=22+22=8;而CQ2=1,PC2=32=9,
∴PC2=PQ2+CQ2,∠PQC=90°,
∵∠PQD=45°,
∴∠CQD=135°,
∴∠APD=∠CQD=135°,
故选:C.
点评 此题主要考查了旋转变换的性质、勾股定理的逆定理等知识点的应用问题;解题的关键是作旋转变换,将分散的条件集中.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运输单位 | 运输速度 (千米/时) | 运费单价 元/(吨•千米) | 运输途中冷藏 元/(吨•时) | 装卸总费用(元) |
| 汽车货运公司 | 75 | 1.5 | 5 | 4000 |
| 火车货运站 | 100 | 1.3 | 5 | 6600 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
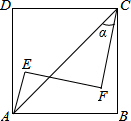 如图,正方形ABCD内有两点E、F满足AE=4,tanα=$\frac{3}{4}$,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为10$\sqrt{2}$.
如图,正方形ABCD内有两点E、F满足AE=4,tanα=$\frac{3}{4}$,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为10$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
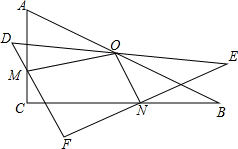 如图,O是Rt△ABC斜边上的中点,将△ABC绕点O旋转至△DEF位置,对应边DF与AC交于点M,对应边EF与BC交于点N.求证:0M⊥0N.
如图,O是Rt△ABC斜边上的中点,将△ABC绕点O旋转至△DEF位置,对应边DF与AC交于点M,对应边EF与BC交于点N.求证:0M⊥0N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com