
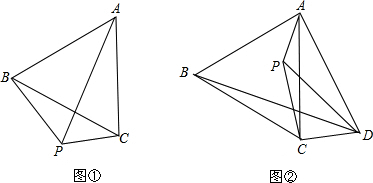
分析 (1)先写出线段BP、PC、AP之间的数量关系,然后根据猜想作出合适的辅助线,画出相应的图形,找出所求数量关系需要的条件即可;
(2)要证明PA+PD+PC>BD,只需要作辅助线延长DP到M使得PM=PA,连接AM、BM,画出相应的图形,根据三角形两边之和大于第三边即可证明结论;
(3)要求BD的长,根据(2)中得到的结论和题意可以得到∠BMD=90°,BM的长,MD的长,然后根据勾股定理即可求得BD的长,本题得以解决.
解答 (1)AP=BP+PC,
证明:延长BP至E,使PE=PC,连接CE,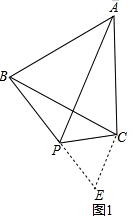 如图1所示,
如图1所示,
∵∠BPC=120°,
∴∠CPE=60°,
又∵PE=PC,
∴△CPE为等边三角形,
∴CP=PE=CE,∠PCE=60°,
∵△ABC为等边三角形,
∴AC=BC,∠BCA=60°,
∴∠ACB=∠PCE,
∴∠ACB+∠BCP=∠PCE+∠BCP,
即∠ACP=∠BCE,
在△ACP与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACP=∠BCE}\\{PC=EC}\end{array}\right.$,
∴△ACP≌△BCE(SAS),
∴AP=BE,
∵BE=BP+PE,
∴AP=BP+PC;
(2)证明:延长DP到M使得PM=PA,连接AM、BM,如下图2所示,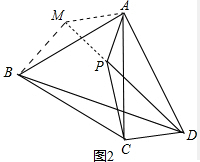
∵∠APD=120°,PM=PA,
∴∠APM=60°,
∴△APM是等边三角形,
∴AM=AP,∠PAM=60°,
∴DM=PD+PA,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠MAP=∠BAC,
∴∠MAP-∠BAP=∠BAC-∠BAP,
即∠MAB=∠PAC,
在△AMB和△APC中,
$\left\{\begin{array}{l}{AM=AP}\\{∠MAB=∠PAC}\\{AB=AC}\end{array}\right.$
∴△AMB≌△APC(SAS)
∴BM=PC,
∵在△BDM中,DM+BM>BD,DM=PD+PA,
∴PA+PD+PC>BD.
(3)如下图2所示,
由(2)知△AMB≌△APC,
∴MB=PC,∠AMB=∠APC,
∵∠CPD=30°,AP=4,CP=5,DP=8,∠APD=120°,∠AMP=60°,
∴MB=5,∠AMB=∠APC=∠APD+∠CPD=120°+30°=150°,
∴∠BMD=∠AMB-∠AMP=90°,
∵MD=MP+PD=4+8=12,MB=5,
∴BD=$\sqrt{M{D}^{2}+M{B}^{2}}=\sqrt{{5}^{2}+1{2}^{2}}=13$,
故答案为:13.
点评 本题主要考查几何变换、对等边三角形的性质和判定,全等三角形的性质和判定,三角形的三边关系,等式的性质等知识点的理解和掌握,此题是一个拔高的题目,有一定的难度,解题的关键是明确题意,作出合适的辅助线,画出相应的图形,利用数形结合的思想解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,有下列四个条件:①AB=BE;②DE⊥DC;③∠ADB=90°;④CE⊥DE.如果添加其中一个条件就能使四边形DBCE成为矩形,那么这个条件是①或③或④.
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,有下列四个条件:①AB=BE;②DE⊥DC;③∠ADB=90°;④CE⊥DE.如果添加其中一个条件就能使四边形DBCE成为矩形,那么这个条件是①或③或④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运输单位 | 运输速度 (千米/时) | 运费单价 元/(吨•千米) | 运输途中冷藏 元/(吨•时) | 装卸总费用(元) |
| 汽车货运公司 | 75 | 1.5 | 5 | 4000 |
| 火车货运站 | 100 | 1.3 | 5 | 6600 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
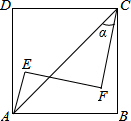 如图,正方形ABCD内有两点E、F满足AE=4,tanα=$\frac{3}{4}$,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为10$\sqrt{2}$.
如图,正方形ABCD内有两点E、F满足AE=4,tanα=$\frac{3}{4}$,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为10$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
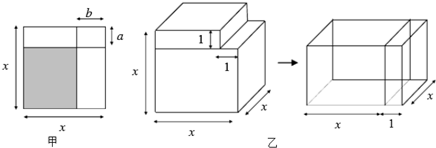
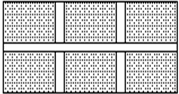 如图,在一条长9米,宽6米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为7米2的6个矩形小块.设小路的宽度为x米,则列方程为(9-2x)(6-x)=42.
如图,在一条长9米,宽6米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为7米2的6个矩形小块.设小路的宽度为x米,则列方程为(9-2x)(6-x)=42.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com