
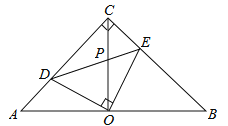
【题目】如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
(1)图形中全等的三角形只有两对;
(2)△ABC的面积等于四边形CDOE的面积的2倍;
(3)CD+CE=![]() OA;
OA;
(4)AD2+BE2=2OPOC.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】解:结论(1)错误.理由如下:
图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.
由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.
∵OC⊥AB,OD⊥OE,∴∠AOD=∠COE.
在△AOD与△COE中,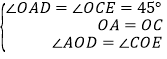
∴△AOD≌△COE(ASA).
同理可证:△COD≌△BOE.
结论(2)正确.理由如下:
∵△AOD≌△COE,∴S△AOD=S△COE,∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=![]() S△ABC,即△ABC的面积等于四边形CDOE的面积的2倍.
S△ABC,即△ABC的面积等于四边形CDOE的面积的2倍.
结论(3)正确,理由如下:
∵△AOD≌△COE,∴CE=AD,∴CD+CE=CD+AD=AC=![]() OA.
OA.
结论(4)正确,理由如下:
∵△AOD≌△COE,∴AD=CE;∵△COD≌△BOE,∴BE=CD.
在Rt△CDE中,由勾股定理得:CD2+CE2=DE2,∴AD2+BE2=DE2.
∵△AOD≌△COE,∴OD=OE.又∵OD⊥OE,∴△DOE为等腰直角三角形,∴DE2=2OE2,∠DEO=45°.∵∠DEO=∠OCE=45°,∠COE=∠COE,∴△OEP∽△OCE,∴![]() ,即OPOC=OE2,∴DE2=2OE2=2OPOC,∴AD2+BE2=2OPOC.
,即OPOC=OE2,∴DE2=2OE2=2OPOC,∴AD2+BE2=2OPOC.
综上所述:正确的结论有3个.故选C.


科目:初中数学 来源: 题型:
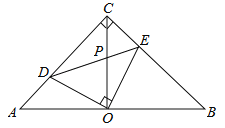
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
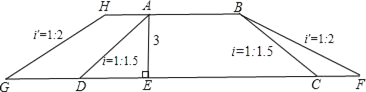
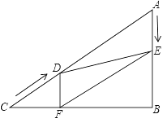
【题目】如图,铁路的路基是等腰梯形ABCD,斜坡AD、BC的坡度i=1:1.5,路基AE高为3米,现由单线改为复线,路基需加宽4米,(即AH=4米),加宽后也成等腰梯形,且GH、BF斜坡的坡度i'=1:2,若路长为10000米,则加宽的土石方量共是____立方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠B=900,AC=100cm, ∠A=600,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒(0<t≤25)过点D作DF⊥BC于点F,连结DE、EF。
(1)四边形AEFD能够成为菱形吗?若能,求相应的t值,若不能,请说明理由。
(2)当t为何值时,△DEF为直角三角形?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福林制衣厂现有24名制作服装的工人,每天都制作某种品牌的衬衫和裤子,每人每天可制作这种衬衫3件或裤子5条.
(1)若该厂要求每天制作的衬衫和裤子数量相等,则应各安排多少人制作衬衫和裤子?
(2)已知制作一件衬衫可获得利润30元,制作一条裤子可获得利润16元,若该厂要求每天获得利润2100元,则需要安排多少名工人制作衬衫?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xoy中,点P的坐标为(m+1,m-1).
(1)试判断点P是否在一次函数y=x-2的图象上,并说明理由;
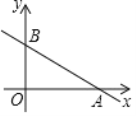
(2)如图,一次函数y= -![]() x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
(3)若点P在直线AB上,已知点R(![]() ,
,![]() ),S(
),S(![]() ,
,![]() )在直线y=kx+b上,b>2,
)在直线y=kx+b上,b>2,![]() +
+![]() =mb,
=mb, ![]() +
+![]() =kb+4若
=kb+4若![]() >
>![]() ,判断
,判断![]() 与
与![]() 的大小关系
的大小关系
查看答案和解析>>
科目:初中数学 来源: 题型:
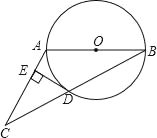
【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=120°,⊙O的半径等于5,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com