
【题目】在“全国爱眼日”这天,某校课题小组为了了解本校![]() 名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
组别 | 视力 | 频率 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
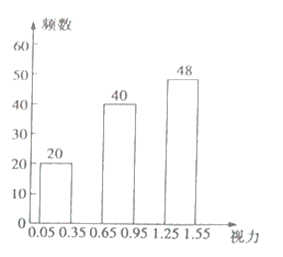
根据以上信息解答下列问题:
![]() 填空:
填空:![]() ______ _,并将频数分布直方图补充完整;
______ _,并将频数分布直方图补充完整;
![]() 若将统计结果绘制成扇形统计图,则第
若将统计结果绘制成扇形统计图,则第![]() 组所在扇形的圆心角度数为 ;
组所在扇形的圆心角度数为 ;
![]() 课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
视力 |
|
|
|
|
|
比重 |
|
|
|
|
|
根据调查结果估计该校有多少名学生的视力下降是由于过度使用电子产品.
【答案】(1)0.18,补全图形见解析;(2)86.4°;(3)215名
【解析】
(1)根据频率值和为1,利用总调查人数等于所占人数除以所占百分比计算即可得到答案;
(2)根据总度数为360°,乘以所占比例即可得到答案;
(3)根据权重的计算公式,即可得到答案
(1)![]() 根据频率之和为1,结合表格的信息得:
根据频率之和为1,结合表格的信息得:
![]() ,
,
总抽查人数为:![]() (人),
(人),
故视力在![]() 的人数为:
的人数为:![]() (人),
(人),
视力在![]() 的人数为:200-20-36-40-48=56(人),
的人数为:200-20-36-40-48=56(人),
补全频数分布直方图如图所示.
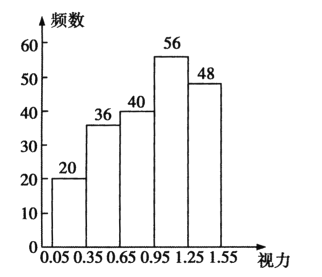
(2)第五组人数的频率是0.24,
∵总扇形度数为360°,
故第五组所占圆心角度数为:
![]() ;
;
![]() 调查的学生中,过度使用电子产品而造成视力下降的学生人数为:
调查的学生中,过度使用电子产品而造成视力下降的学生人数为:![]() ,
,
因为学校总人数为1000,故估计该校因过度使用电子产品而造成视力下降的学生有:
![]() (名).
(名).


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
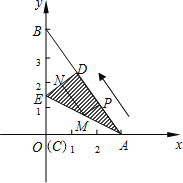
【题目】如图所示,Rt△ABC是一张放在平面直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4.将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上.
(1)在下图所示的直角坐标系中,求E点的坐标及AE的长.
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值时,A、D、M三点构成等腰三角形?并求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:

(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】篮球运动是全世界最流行的运动之一,近年流行于青少年之间的“3对3”篮球将登上2020年奥运会赛场,为备战某市中学生“3对3”篮球联赛,某校甲、乙、丙三位同学作为“兄弟战队”的主力队员进行篮球传球训练,篮球由一个人随机传给另一个人,且每位传球人传球给其余两人的机会是均等的,现在由甲开始传球.
(1)求甲第一次传球给乙的概率;
(2)三次传球后,篮球在谁手中的可能性大?请利用树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.
(1)求y关于x的函数表达式.
(2)若购进A种的数量不少于B种的数量.
①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有______本(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
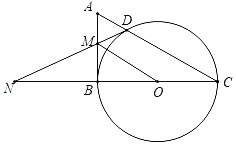
【题目】如图,在Rt△ABC中,以BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点M,交CB延长线于点N,连接OM,OC=1.
(1)求证:AM=MD;
(2)填空:
①若DN![]() ,则△ABC的面积为 ;
,则△ABC的面积为 ;
②当四边形COMD为平行四边形时,∠C的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
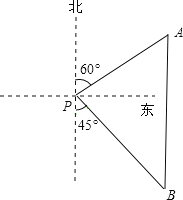
【题目】如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com