
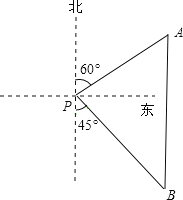
【题目】如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号).
科目:初中数学 来源: 题型:
【题目】在“全国爱眼日”这天,某校课题小组为了了解本校![]() 名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
组别 | 视力 | 频率 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
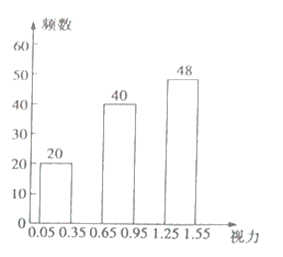
根据以上信息解答下列问题:
![]() 填空:
填空:![]() ______ _,并将频数分布直方图补充完整;
______ _,并将频数分布直方图补充完整;
![]() 若将统计结果绘制成扇形统计图,则第
若将统计结果绘制成扇形统计图,则第![]() 组所在扇形的圆心角度数为 ;
组所在扇形的圆心角度数为 ;
![]() 课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
视力 |
|
|
|
|
|
比重 |
|
|
|
|
|
根据调查结果估计该校有多少名学生的视力下降是由于过度使用电子产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,并经过点
,并经过点![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() .将抛物线
.将抛物线![]() 平移后得到顶点为
平移后得到顶点为![]() 且对称轴为直线
且对称轴为直线![]() 的抛物线
的抛物线![]() .
.
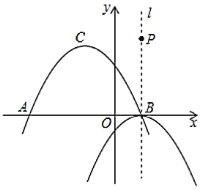
(1)求抛物线![]() 的表达式;
的表达式;
(2)在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请求出所有点
为等腰三角形?若存在,请求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
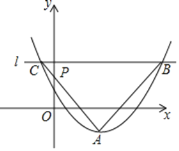
【题目】如图,在平面直角坐标系中,抛物线y=![]() -1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
-1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,D、E是AB、BC上两点,将△ABC沿DE折叠,使点B落在AC边上点F处,并且DF∥BC,若CF=3,BC=9,则AB的长是( )
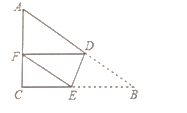
A. ![]() B. 15C.
B. 15C. ![]() D. 9
D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,等腰直角三角形![]() 与
与![]() 的顶点都在网格点上,点
的顶点都在网格点上,点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上的动点,且
上的动点,且![]() .
.
(Ⅰ)如图①,当![]() 时,计算
时,计算![]() 的值等于__;
的值等于__;
(Ⅱ)当![]() 取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段
取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段![]() 和
和![]() ,并简要说明点
,并简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明).
的位置是如何找到的(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,点A、B均为格点.
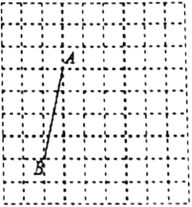
(Ⅰ)AB的长等于_____.
(Ⅱ)若点C是以AB为底边的等腰直角三角形的顶点,点D在边AC上,且满足S△ABD=![]() S△ABC.请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置是如何找到的(不要求证明)______.
S△ABC.请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目:初中数学 来源: 题型:
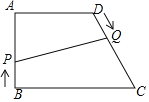
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=AD=8cm,CD=10cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为lcm/s.连接PQ,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,PQ∥AD?
(2)设四边形APQD的面积为y(cm2),求y与t的函数关系式;
(3)是否存在某一时刻t,使S四边形APQO:S四边形BCQP=17:27?若存在,求出t的值,并求此时PQ的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com