
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,
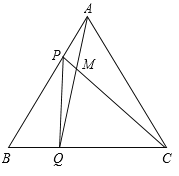
(1)求证:△ABQ ≌ △CAP;
(2)∠CMQ的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)连接PQ,当点P、Q运动多少秒时,△APQ是等腰三角形?
【答案】(1)证明见解析;(2)∠CMQ的大小不变且为60度;(3)t=2.
【解析】
(1)根据等边三角形的性质、三角形全等的判定定理证明;
(2)根据全等三角形的性质得到∠BAQ=∠ACP,根据三角形的外角的性质解答;
(3)分三种情况分别讨论即可求解.
(1)根据路程=速度×时间可得:AP=BQ
∵△ABC是等边三角形
∴∠PAC=∠B=60°,AB=AC
∴△ABQ≌△CAP(SAS)
(2)∵ △ABQ≌△CAP
∴∠BAQ=∠ACP
∴∠CMQ=∠ACM+∠MAC=∠BAQ+∠MAC=60°
因此,∠CMQ的大小不变且为60度
(3)当AP=AQ时,仅当P运动到B点,Q运动到C点成立,故不符合题意;
当PQ=AQ时,仅当P运动到B点,Q运动到C点成立,故不符合题意;
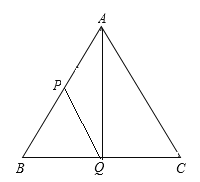
当AP=PQ时,如图,当AQ⊥BC时,AP=BP=PQ,故t=2÷1=2时,△APQ为等腰三角形;
综上,当t=2时,△APQ为等腰三角形,此时AP=PQ.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字![]() ,
,![]() ,
,![]() ,现将标有数字的一面朝下.小明和小亮各从中任意抽取一张.计算小明和小亮抽得的两个数字之和,如果和为奇数则小明胜,和为偶数则小亮胜.
,现将标有数字的一面朝下.小明和小亮各从中任意抽取一张.计算小明和小亮抽得的两个数字之和,如果和为奇数则小明胜,和为偶数则小亮胜.
![]() 求小亮抽到标有数字
求小亮抽到标有数字![]() 卡片取胜的概率;
卡片取胜的概率;
![]() 请判断该游戏对双方是否公平?请用列表法或树状图等方法说明理由.
请判断该游戏对双方是否公平?请用列表法或树状图等方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD,墙长28m.设AB长为xm,矩形的面积为ym2.
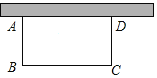
(1)写出y与x的函数关系式;
(2)当AB长为多少米时,所围成的花圃面积最大?最大值是多少?
(3)当花圃的面积为150m2时,AB长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
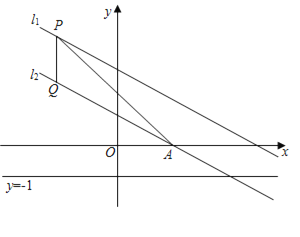
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+2向下平移1个单位后,得到直线l2,l2交x轴于点A,点P是直线l1上一动点,过点P作PQ∥y轴交l2于点Q
x+2向下平移1个单位后,得到直线l2,l2交x轴于点A,点P是直线l1上一动点,过点P作PQ∥y轴交l2于点Q
(1)求出点A的坐标;
(2)连接AP,当△APQ为以PQ为底边的等腰三角形时,求点P和点Q的坐标;
(3)点B为OA的中点,连接OQ、BQ,若点P在y轴的左侧,M为直线y=﹣1上一动点,当△PQM与△BOQ全等时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.

依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
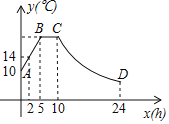
【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,对于任意两点![]() ,
,![]() ,若点
,若点![]() 满足
满足![]() ,
,![]() ,那么称点
,那么称点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
例如:![]() ,
,![]() ,当点
,当点![]() 满是
满是![]() ,
,![]() 时,则点
时,则点![]() 是点
是点![]() ,
,![]() 的融合点,
的融合点,

(1)已知点![]() ,
,![]() ,
,![]() ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.
(2)如图,点![]() ,点
,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
①试确定![]() 与
与![]() 的关系式.
的关系式.
②若直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
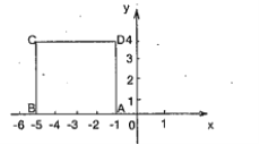
【题目】如图,将边长为![]() 的正方形放在平面直角坐标系第二象限,使
的正方形放在平面直角坐标系第二象限,使![]() 边落在
边落在![]() 轴负半轴上,且点
轴负半轴上,且点![]() 的坐标是
的坐标是![]() .
.
(1)直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(2)若直线![]() 经过点
经过点![]() ,且将正方形
,且将正方形![]() 分成面积相等的两部分,求直线
分成面积相等的两部分,求直线![]() 的解析式;
的解析式;
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行.将(2)中直线
平行.将(2)中直线![]() 沿着
沿着![]() 轴向上平移
轴向上平移![]() 个单位,交
个单位,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com