
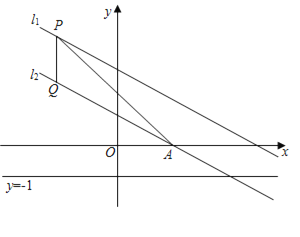
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+2向下平移1个单位后,得到直线l2,l2交x轴于点A,点P是直线l1上一动点,过点P作PQ∥y轴交l2于点Q
x+2向下平移1个单位后,得到直线l2,l2交x轴于点A,点P是直线l1上一动点,过点P作PQ∥y轴交l2于点Q
(1)求出点A的坐标;
(2)连接AP,当△APQ为以PQ为底边的等腰三角形时,求点P和点Q的坐标;
(3)点B为OA的中点,连接OQ、BQ,若点P在y轴的左侧,M为直线y=﹣1上一动点,当△PQM与△BOQ全等时,求点M的坐标.
【答案】(1)A(2,0);(2)P(3,![]() ),Q(3,﹣
),Q(3,﹣![]() );(3)M(﹣1,﹣1)或(﹣1,8)
);(3)M(﹣1,﹣1)或(﹣1,8)
【解析】
(1)求出直线l2的解析式为y=﹣![]() x+1,即可求A的坐标;
x+1,即可求A的坐标;
(2)设点P(x,﹣![]() x+2),Q(x,﹣
x+2),Q(x,﹣![]() x+1),由AQ=AP,即可求P点坐标;
x+1),由AQ=AP,即可求P点坐标;
(3)设P(n,﹣![]() n+2),M(m,﹣1),则Q(n,﹣
n+2),M(m,﹣1),则Q(n,﹣![]() n+1),可求出BQ=
n+1),可求出BQ=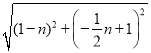 ,OQ=
,OQ=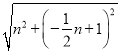 ,PM=
,PM=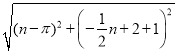 ,QM=
,QM=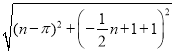 ,①当△PQM≌△BOQ时,PM=BQ,QM=OQ,结合勾股定理,求出m;②当△QPM≌△BOQ时,有PM=OQ,QM=BQ,结合勾股定理,求出m即可.
,①当△PQM≌△BOQ时,PM=BQ,QM=OQ,结合勾股定理,求出m;②当△QPM≌△BOQ时,有PM=OQ,QM=BQ,结合勾股定理,求出m即可.
解:(1)∵直线l1:y=﹣![]() x+2向下平移1个单位后,得到直线l2,
x+2向下平移1个单位后,得到直线l2,
∴直线l2的解析式为y=﹣![]() x+1,
x+1,
∵l2交x轴于点A,
∴A(2,0);
(2)当△APQ为以PQ为底边的等腰三角形时,
∴AQ=AP,
∵点P是直线l1上一动点,
设点P(x,﹣![]() x+2),
x+2),
∵过点P作PQ∥y轴交l2于点Q
∴Q(x,﹣![]() x+1),
x+1),
∴(﹣![]() x+2)2=(﹣
x+2)2=(﹣![]() x+1)2,
x+1)2,
∴x=3,
∴P(3,![]() ),Q(3,﹣
),Q(3,﹣![]() );
);
(3)∵点B为OA的中点,
∴B(1,0),
∴PQ=BO=1,
设P(n,﹣![]() n+2),M(m,﹣1),则Q(n,﹣
n+2),M(m,﹣1),则Q(n,﹣![]() n+1),
n+1),
∴BQ=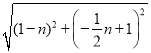 ,OQ=
,OQ=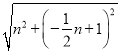 ,
,
PM=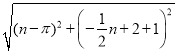 ,QM=
,QM=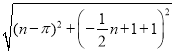 ,①
,①
∵△PQM与△BOQ全等,
①当△PQM≌△BOQ时,
有PM=BQ,QM=OQ,
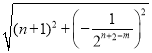 =
=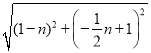 ,
,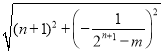 =
=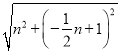 ,
,
∴n=2m﹣2,
∵点P在y轴的左侧,
∴n<0,
∴m<1,
∴m=﹣1,
∴M(﹣1,﹣1);
②当△QPM≌△BOQ时,
有PM=OQ,QM=BQ,
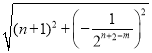 =
=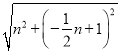 ,
,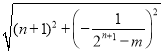 =
=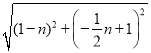 ,
,
∴n=![]() ﹣
﹣![]() m,
m,
∵点P在y轴的左侧,
∴n<0,
∴m>2,
∴m=8,
∴M(﹣1,8);
综上所述,M(﹣1,﹣1)或M(﹣1,8).1:y=﹣![]() x+2向下平移1个单位后,得到直线l2,
x+2向下平移1个单位后,得到直线l2,


科目:初中数学 来源: 题型:
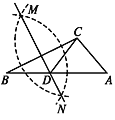
【题目】如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于![]() BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
A.90°B.95°C.105°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
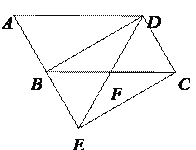
(1)求证:△BEF≌△CDF.
(2)连接BD,CE,若∠BFD=2∠A,求证四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一组数据![]() ,
,![]() ,
,![]() 中,各数据与它们的平均数
中,各数据与它们的平均数![]() 的差的绝对值的平均数,记作
的差的绝对值的平均数,记作![]() 叫做这组数据的“平均差”.一组数据的平均差越大,就说明这组数据的离散程度越大.则样本:
叫做这组数据的“平均差”.一组数据的平均差越大,就说明这组数据的离散程度越大.则样本:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的平均差是( )
的平均差是( )
A. ![]() B. 3 C. 6 D.
B. 3 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,
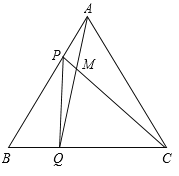
(1)求证:△ABQ ≌ △CAP;
(2)∠CMQ的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)连接PQ,当点P、Q运动多少秒时,△APQ是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如右表所示:图二是某同学根据上表绘制的一个不完整的条形图.请你根据以上信息解答下列问题:
(1)补全图一和图二.
(2)请计算每名候选人的得票数.
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 在平面直角坐标系中的位置如图所示,将
在平面直角坐标系中的位置如图所示,将![]() 向右平移5个单位长度,再向下平移3个单位长度得到
向右平移5个单位长度,再向下平移3个单位长度得到![]() .(图中每个小方格边长均为1个单位长度)
.(图中每个小方格边长均为1个单位长度)
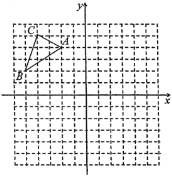
(1)在图中画出平移后的![]() ;
;
(2)直接写出![]() 各顶点的坐标
各顶点的坐标![]() ______,
______,![]() ______,
______,![]() ______.
______.
(3)在![]() 轴上找到一点
轴上找到一点![]() ,当
,当![]() 取最小值时,
取最小值时,![]() 点的坐标是______.
点的坐标是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com