
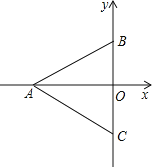
【题目】如图,等边![]() 的顶点
的顶点![]() ,顶点
,顶点![]() 、
、![]() 在
在![]() 轴上.
轴上.
(1)写出![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)求![]() 的面积和周长.
的面积和周长.
【答案】(1)B(0,4) C(0,-4);(2)![]() ,24.
,24.
【解析】
(1)由等边三角形的性质可知原点是BC的中点,AB=2BO,在Rt△AOB中,由勾股定理可求得BO,OC的长,从而得出B,C的坐标;
(2)根据B、C的坐标求得等边三角形ABC的边长,然后根据面积公式和周长公式即可求得结果.
解:(1)∵△ABC是等边三角形,![]() 轴⊥
轴⊥![]() 轴,
轴,
∴∠BAO=30°,BO=OC,
∴AB=2BO.
在Rt△AOB中,由勾股定理得![]() ,
,
又∵A(![]() ),∴AO=
),∴AO=![]() ,
,
∴![]() ,
,
∴BO=4,∴OC=OB=4.
∴点B,C的坐标分别为B(0,4),C(0,-4);
(2)由(1)得B(0,4),C(0,-4),
∴BC=8,
∴![]() =
=![]() =
=![]() ;
;
∴![]() .
.
故![]() 的面积为
的面积为![]() ,周长为24.
,周长为24.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
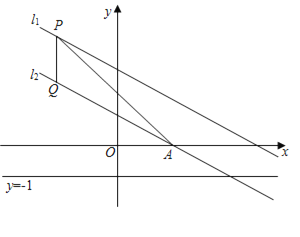
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+2向下平移1个单位后,得到直线l2,l2交x轴于点A,点P是直线l1上一动点,过点P作PQ∥y轴交l2于点Q
x+2向下平移1个单位后,得到直线l2,l2交x轴于点A,点P是直线l1上一动点,过点P作PQ∥y轴交l2于点Q
(1)求出点A的坐标;
(2)连接AP,当△APQ为以PQ为底边的等腰三角形时,求点P和点Q的坐标;
(3)点B为OA的中点,连接OQ、BQ,若点P在y轴的左侧,M为直线y=﹣1上一动点,当△PQM与△BOQ全等时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:2019年11月2日-4日,江西省中小学生研学实践教育推进会和全国中小学综合实践活动(研学实践教育)论坛相继在抚州举行.为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,抚州市某中学决定组织部分班级去仙盖山开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.参加此次研学旅行活动的老师和学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校八年级学生参加体育锻炼的情况,随机调查了该校部分学生每周参加体育锻炼的时间,并进行了统计,绘制成图1和图2两幅尚不完整的统计图.
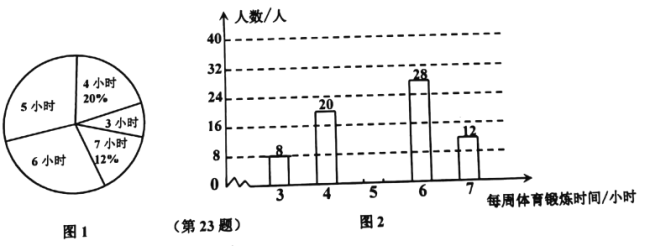
(1)本次共调查学生 人;
(2)这组数据的众数是 ;
(3)请你将图2的统计图补充完整;
(4)若该校八年级共有650人,请根据样本数据,估计每周参加体育锻炼时间为6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的正方形放在平面直角坐标系第二象限,使
的正方形放在平面直角坐标系第二象限,使![]() 边落在
边落在![]() 轴负半轴上,且点
轴负半轴上,且点![]() 的坐标是
的坐标是![]() .
.
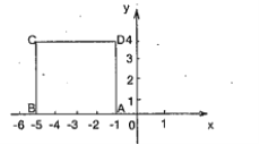
(1)直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(2)若直线![]() 经过点
经过点![]() ,且将正方形
,且将正方形![]() 分成面积相等的两部分,求直线
分成面积相等的两部分,求直线![]() 的解析式;
的解析式;
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行.将(2)中直线
平行.将(2)中直线![]() 沿着
沿着![]() 轴向上平移
轴向上平移![]() 个单位,交
个单位,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两实根,实数
的两实根,实数![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系可能是( )
的大小关系可能是( )
A. α<a<b<β B. a<α<β<b C. a<α<b<β D. α<a<β<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与
与x轴交于A、B两点,与![]() 轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.
轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.

(1)求抛物线所对应的函数解析式.
(2)若点P为抛物线对称轴上的一个动点,求![]() PAC周长的最小值.
PAC周长的最小值.
(3)将AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 为直线
为直线![]() 上一点,
上一点,![]() 为直线外一点,连结
为直线外一点,连结![]() .
.
(1)用直尺、圆规在直线![]() 上作点
上作点![]() ,使
,使![]() 为等腰三角形(作出所有符合条件的点
为等腰三角形(作出所有符合条件的点![]() ,保留痕迹).
,保留痕迹).
(2)设![]() ,若(1)中符合条件的点
,若(1)中符合条件的点![]() 只有两点,直接写出
只有两点,直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com