
 һ����ֱ�Ĺ�·����A��B��C���أ�B��C�������150ǧ�ף��ס������������ֱ��B��C����ͬʱ�������ع�·����������У��ֱ�ʻ��C��B���أ��ס���������A�صľ���y1��y2��km������ʻʱ��x��h���Ĺ�ϵ��ͼ��ʾ������ͼ���������̽����
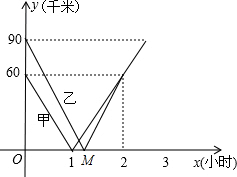
һ����ֱ�Ĺ�·����A��B��C���أ�B��C�������150ǧ�ף��ס������������ֱ��B��C����ͬʱ�������ع�·����������У��ֱ�ʻ��C��B���أ��ס���������A�صľ���y1��y2��km������ʻʱ��x��h���Ĺ�ϵ��ͼ��ʾ������ͼ���������̽�������� ��1������ͼʾ������֪��A����AB��AC=2��3���ɵ�AC�ľ��룬ֱ�Ӹ���������ʽ�����ҳ����ٶ�150��2=75ǧ��/ʱ��90��75=1.2�����Ե�M��ʾ�ҳ�1.2Сʱ����A�أ�
��2������ͼ���֪ͼ���ϵ�����꣬���������Ա���ȡֵ��Χ���������ϵʽ���ɣ�
��3����ͼ��ֱ�����1��x��1.2ʱ��x��1.2ʱ�ס��ҵĽ���ʽ��������ȣ��Ӷ����ʱ�䣻
��4�����ݡ������Խ�����15ǧ��֮�ڣ���15ǧ�ף�ʱ�ܹ�����ͨ������Ϊ���ȹ�ϵ�в���ʽ�飬��⼴�ɵõ�ͨ����ʱ�䷶Χ�����Կ�������ͬʱ��ָ������ͨ����ʱ��Ϊ$\frac{5}{4}$-1=$\frac{1}{4}$Сʱ
��� �⣺��1����ͼ��ɵã�AC=BC-AB=150-60=90km��
�ҳ����ٶ�150��2=75ǧ��/ʱ��
90��75=1.2��
��M��1.2��0����
�ʴ�Ϊ��90����1.2��0����
��2���׳��ĺ���ͼ����ͼ��ʾ���׳����ٶ�60��1=60��ǧ��/ʱ����
�׳���B��C����ʱ��Ϊ��150��60=2.5��Сʱ����
����0��60������1��0��������y1=kx+b��
�ã�$\left\{\begin{array}{l}{b=60}\\{k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-60}\\{b=60}\end{array}\right.$��
�ʵ�0��x��1ʱ��y1=-60x+60��
����2.5��90������1��0��������y1=ax+c��
$\left\{\begin{array}{l}{2.5a+c=90}\\{a+c=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=60}\\{c=-60}\end{array}\right.$��
�ʵ�1��x��2.5ʱ��y1=60x-60��
��ͼ�в�ȫ�׳��ĺ���ͼ��Ϊ��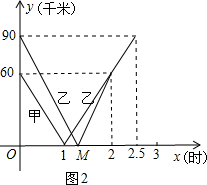
��3����ͼ��֪����1��x��1.2ʱ���׳�����C�㣬�ҳ���δ����C�㣬�ɵ�
y=-75x+90=60x-60��
���x=$\frac{10}{9}$��
��x��1.2ʱ�У�
y=75x-90=60x-60��
���x=2��
��������ʻ$\frac{10}{9}$��2��Сʱ��C�ؾ�����ȣ�
��4��������ü׳���ָ�����ĵ�ͨ��ʱ��Ϊ��
$\left\{\begin{array}{l}{60x-60��15}\\{-60x+60��15}\end{array}\right.$��
��$\frac{3}{4}$��x��$\frac{5}{4}$��
�ҳ���ָ�����ĵ�ͨ��ʱ�䣺$\left\{\begin{array}{l}{-75x+90��15}\\{75x-90��15}\end{array}\right.$��
��1��x��$\frac{7}{5}$��
��1��x��$\frac{5}{4}$��
������ͬʱ��ָ������ͨ����ʱ��Ϊ$\frac{5}{4}$-1=$\frac{1}{4}$Сʱ��
���� ������Ҫ��������һ�κ�����ģ�ͽ��ʵ������������Ͷ�ͼ������Ҫ�ȸ��������г�������ϵʽ���ٴ�����ֵ������Ĺؼ���Ҫ�����������ʵ������ȷ���г�����ʽ���ٰѶ�Ӧֵ������⣬�������ͼʾ�ó�����Ҫ����Ϣ��


 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+$\frac{1}{x}$=$\frac{1+{x}^{2}}{x}$ | B�� | ��x-3��2=x2-9 | C�� | x2-x=x��x-1�� | D�� | |x-1|2=��x-1��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
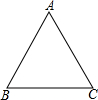 ���ڱ߳�Ϊ10����������ABC�������ʵ���ֱ������ϵ��д��������������꣮
���ڱ߳�Ϊ10����������ABC�������ʵ���ֱ������ϵ��д��������������꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪��A��B�������260ǧ�ף��׳���A��ǰ��B���������ʣ���ʻ2Сʱ��M���������ֹ��ϣ�����֪ͨ������Ա���ҳ���A�и���ά�ޣ�֪ͨʱ����Բ��ƣ����ҳ�����M�غ��־���20�����ü׳�����ԭ��ԭ·���أ�ͬʱ�׳���ԭ��1.5�����ٶ�ǰ��B�У���ͼ��������A�е�·��y��ǧ�ף���׳���ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ����Ϣ�ó����½��ۣ��ټ׳����ٺ���ٶ���60ǧ��/ʱ�����ҳ����ٶ���96ǧ��/ʱ���۵�C������Ϊ��$\frac{19}{6}$��80�����ܼ׳�����B��ʱ�ҳ��ѷ���A��2Сʱ������Ϊ��ȷ�Ľ����У�����������
��֪��A��B�������260ǧ�ף��׳���A��ǰ��B���������ʣ���ʻ2Сʱ��M���������ֹ��ϣ�����֪ͨ������Ա���ҳ���A�и���ά�ޣ�֪ͨʱ����Բ��ƣ����ҳ�����M�غ��־���20�����ü׳�����ԭ��ԭ·���أ�ͬʱ�׳���ԭ��1.5�����ٶ�ǰ��B�У���ͼ��������A�е�·��y��ǧ�ף���׳���ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ����Ϣ�ó����½��ۣ��ټ׳����ٺ���ٶ���60ǧ��/ʱ�����ҳ����ٶ���96ǧ��/ʱ���۵�C������Ϊ��$\frac{19}{6}$��80�����ܼ׳�����B��ʱ�ҳ��ѷ���A��2Сʱ������Ϊ��ȷ�Ľ����У�����������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
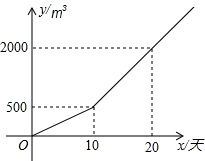 ijũ����ֲһ�־������������ˮ��y��m3������ֲʱ��x���죩֮��ĺ�����ϵ��ͼ��ʾ��
ijũ����ֲһ�־������������ˮ��y��m3������ֲʱ��x���죩֮��ĺ�����ϵ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com