
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P��a��b��������P1������Ϊ��a+kb��ka+b��������kΪ��������k��0������Ƶ�P1Ϊ��P����k������������
���磬P��1��4������2����������ΪP1��1+2��4��2��1+4������P1��9��6����
��1���㣨��2��3������3����������P1������Ϊ�� ����ֱ����գ�
��2������P����5����������P1������Ϊ��3����9�������P����Ϊ�� ����ֱ����գ���
��3����x����������һ��P��a��0������k����������ΪP1�����߶�PP1�ij���Ϊ�߶�OP���ȵ�2������k���� ����ֱ����գ���
��4���ڣ�3���������£�����M��y���ϣ�����MP��MP1��ʹMP1ƽ�֡�PMO����ֱ��д����M�������꣨�ú�a�Ĵ���ʽ��ʾ����
���𰸡���1����7����3������2������2��1������3����2����4����M��������Ϊ��![]() a��
a��
��������
(1)���������������.
(2)����������������������.
(3)���������г���ʽ�������.
(4)�������⻭��ͼ��, ����P1��P1B��MP,����M��MC��P1P,֤����MCP�ա�P1PB,�������.
�⣺(1)P1(��2+3��3,��2��3+3),��P1(7,��3)��
�ʴ�Ϊ(7,��3)��
(2)�������������:a+5b=3,5a+b=��9,���a=��2,b=1
�ʴ�Ϊ(��2,1)��
(3)P(a,0)����k����������ΪP1(a,ka),
��PP1�ij���Ϊ|ka|,OP����Ϊa,
���߶�PP1�ij���Ϊ�߶�OP���ȵ�2��,
��|ka|��2a,
��k����2,
�ʴ�Ϊ��2��
(4)��k����2,
��P1(a,��2a),
��P1(a,2a)ʱ,
����P1��P1B��MP,����M��MC��P1P,
��MP1ƽ�֡�PMO,
��AP1��P1B��a,
��MC��a,
���MCP�ա�P1PB(AAS),
��MP��P1P��2a,
��PC��![]() a,
a,
���M����������![]() a��
a��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1��![]() ��֤��
��֤��![]()
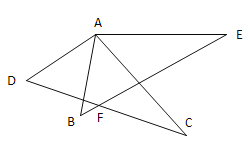
�� ͼ1��
��2����ͼ2��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() Ϊ��������һ�㣬
Ϊ��������һ�㣬![]() ����֤��
����֤��![]()
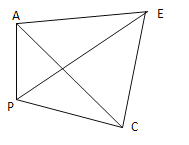
�� ͼ2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Խ��Խ����������Ÿ�������˻����Ǯת�����п��������֣���2016��3��1����ÿ�����˻���������1000Ԫ��������ֶ�ȣ����ۼ����ֽ���1000Ԫʱ�������IJ�����֧��0.1���������ѣ��Ժ�ÿ������֧���������Ѿ�Ϊ���ֽ���0.1����
��1��Сӱ2018�꿪ʼʹ���ţ������Լ������˻���һ�����ֽ��Ϊ2000Ԫ����֧�������� Ԫ��
��2��С����2016��3��1���������Լ������˻����������Σ����ֽ������������£�
��һ�� | �ڶ��� | ������ | |
���ֽ��/Ԫ |
|
|
|
������/Ԫ | 0 | 0.2 | 3.0 |
��ôС�����������ֵĽ��ֱ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���AB�Ķ���A��ϵһ����ģ���ijһʱ�̣���˵�Ӱ������ƽ��BD��һ�¶�Ϊ1��![]() ��б��DF�ϣ���������ʹ��Ӱ����������б�¶���D������������BC=8m��Ӱ��BD=16m��Ӱ��DE=12m�����������AB����洹ֱ��B��D��G���㹲�ߣ�AB��BG��DF��ͬһƽ���ڣ���
��б��DF�ϣ���������ʹ��Ӱ����������б�¶���D������������BC=8m��Ӱ��BD=16m��Ӱ��DE=12m�����������AB����洹ֱ��B��D��G���㹲�ߣ�AB��BG��DF��ͬһƽ���ڣ���
��1�����½ǡ�FDG�Ķ�����
��2�������AB�ĸ߶ȣ���ע��![]() ��1.73�������ȷ��0.1m��
��1.73�������ȷ��0.1m��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����12��10�������������У���ABC�Ǹ�������Σ���B������Ϊ����5��1������C������Ϊ����4��5����
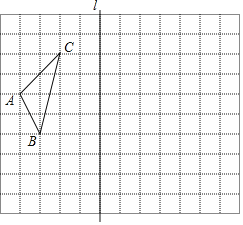
��1�����ڷ���ֽ�л���x�ᡢy�ᣬ�����ԭ��O��
��2��������ABC����ֱ��l�ԳƵ���A1B1C1��
��3������P��a��b������ABC�ڣ������ֱ��l�ĶԳƵ���P1����P1���������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣮�����
���е㣮�����![]() ���߶�
���߶�![]() ����
����![]() ���ٶ��ɵ�
���ٶ��ɵ�![]() ��
��![]() ���˶���ͬʱ����
���˶���ͬʱ����![]() ���߶�
���߶�![]() ���ɵ�
���ɵ�![]() ��
��![]() ���˶���
���˶���

��1������![]() ���˶��ٶ����
���˶��ٶ����![]() ���˶��ٶ���ȣ�����1���
���˶��ٶ���ȣ�����1���![]() ��
��![]() �Ƿ�ȫ�ȣ���˵�����ɣ�
�Ƿ�ȫ�ȣ���˵�����ɣ�
��2������![]() ���˶��ٶ����
���˶��ٶ����![]() ���˶��ٶȲ���ȣ�����
���˶��ٶȲ���ȣ�����![]() ���˶��ٶ�Ϊ����ʱ���ܹ�ʹ
���˶��ٶ�Ϊ����ʱ���ܹ�ʹ![]() ��
��![]() ȫ�ȣ�
ȫ�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ABΪ��O��ֱ����C��D�ǡ�Oֱ��AB�������㣬AC=DC������C���O���е�ֱ��CF����DB���ӳ����ڵ�E��
��1�����ж�ֱ��DE��CF��λ�ù�ϵ����˵�����ɣ�
��2������A=30�㣬AB=4����![]() �ij���
�ij���
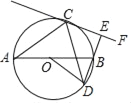
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����ֱ�����������(��ABC�����С�ACB��90��)��������һ�����ڣ���������A��B��C�ֱ����ڰ����ڱ��ϣ���֪��ADE����BED��90�㣬���AD��5cm��BE��7cm���������������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�۸���ѧϰ�����ľ��飬�Ժ���![]() ͼ�������ʽ�����̽����������С�۵�̽�����̣��벹��������
ͼ�������ʽ�����̽����������С�۵�̽�����̣��벹��������
��1����![]() ��
��![]() Ϊ�ú���ͼ���ϲ�ͬ�����㣬��
Ϊ�ú���ͼ���ϲ�ͬ�����㣬��![]() ���ú�������СֵΪ .
���ú�������СֵΪ .
��2����������ϵ�л���ֱ��![]() �뺯��
�뺯��![]() ��ͼ��д����
��ͼ��д����![]() ʱ
ʱ![]() ��ȡֵ��Χ�� .
��ȡֵ��Χ�� .
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com