
【题目】(1)如图1,![]() 求证:
求证:![]()
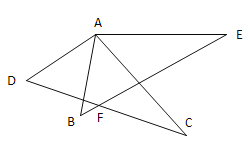
( 图1)
(2)如图2,![]() 是等边三角形,
是等边三角形,![]() 为三角形外一点,
为三角形外一点,![]() ,求证:
,求证:![]()
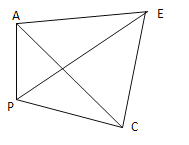
( 图2)
【答案】(1)见解析(2)见解析
【解析】
(1)根据题意证明△ABE≌△ADC即可求解;
(2)延长CP至B,使PB=PA,连接AB,证△APB为等边三角形得AP=PB=AB,再证△△BAC≌△PAE得EP=BC,可得![]() .
.
(1)![]()
∴![]()
即![]()
又![]() ,
,![]()
∴△ABE≌△ADC
∴![]()
(2)如图,延长CP至B,使PB=PA,连接AB,
∵![]()
∴∠APB=60![]() ,又PB=PA,
,又PB=PA,
∴△APB为等边三角形,
∴AP=PB=AB,∠BAP=60![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴AC=AE,∠EAC=60,
∴∠BAP =∠EAC,
∴∠BAP +∠PAC=∠EAC +∠PAC,
即:∠BAC=∠PAE,
在△BAC和△PAE中,
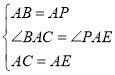
∴△BAC≌△PAE (SAS),
∴BC=PE,
∵BC=BP+PC=AP+ PC,
∴![]() .
.



 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF.若∠EFD=15°,则∠CDF的度数为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应香洲区全面推进书香校园建设的号召,班长小青随机调查了若干同学一周课外阅读的时间t(单位:小时),将获得的数据分成四组,绘制了如下统计图(A:0<t≤7,B:7<t≤14,C:14<t≤21,D:t>21),根据图中信息,解答下列问题:

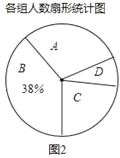
(1)这项工作中被调查的总人数是多少?
(2)补全条形统计图,并求出表示A组的扇形统计图的圆心角的度数;
(3)如果小青想从D组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表,请用列表或树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查,并绘制成如图①②的统计图。已知“查资料”人人数是40人。

请你根据以上信息解答以下问题
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_______________。
(2)补全条形统计图
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的反比例函数,且当x=2时,y=﹣3,
(1)求y与x之间的函数关系式;
(2)画出这个函数的图象;
(3)试判断点P(﹣2,3)是否在这个函数的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
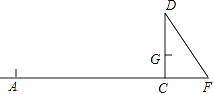
【题目】已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(设A,C,F在同一水平线上).
(1)按比例较精确地作出高楼AB及它的最大影长AE;
(2)问若大楼AB建成后是否影响温室CD的采光,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P1的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P1为点P的“k属派生点”.
例如,P(1,4)的“2属派生点”为P1(1+2×4,2×1+4),即P1(9,6).
(1)点(﹣2,3)的“3属派生点”P1的坐标为 (直接填空)
(2)若点P的“5属派生点”P1的坐标为(3,﹣9),则点P坐标为 (直接填空);
(3)若x轴正半轴上一点P(a,0)的“k属派生点”为P1,且线段PP1的长度为线段OP长度的2倍,则k= (直接填空);
(4)在(3)的条件下,若点M在y轴上,连接MP、MP1,使MP1平分∠PMO,请直接写出点M的纵坐标(用含a的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com