
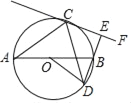
【题目】已知:如图,AB为⊙O的直径,C,D是⊙O直径AB异侧的两点,AC=DC,过点C与⊙O相切的直线CF交弦DB的延长线于点E.
(1)试判断直线DE与CF的位置关系,并说明理由;
(2)若∠A=30°,AB=4,求![]() 的长.
的长.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
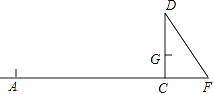
【题目】已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(设A,C,F在同一水平线上).
(1)按比例较精确地作出高楼AB及它的最大影长AE;
(2)问若大楼AB建成后是否影响温室CD的采光,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点A8的坐标为__________.
,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点A8的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P1的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P1为点P的“k属派生点”.
例如,P(1,4)的“2属派生点”为P1(1+2×4,2×1+4),即P1(9,6).
(1)点(﹣2,3)的“3属派生点”P1的坐标为 (直接填空)
(2)若点P的“5属派生点”P1的坐标为(3,﹣9),则点P坐标为 (直接填空);
(3)若x轴正半轴上一点P(a,0)的“k属派生点”为P1,且线段PP1的长度为线段OP长度的2倍,则k= (直接填空);
(4)在(3)的条件下,若点M在y轴上,连接MP、MP1,使MP1平分∠PMO,请直接写出点M的纵坐标(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
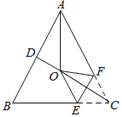
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于![]() BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
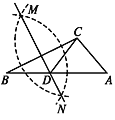
A.90°B.95°C.105°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
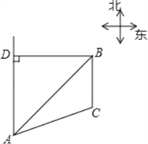
【题目】已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)(参考数据:![]() 1.41,
1.41,![]() 1.73,
1.73,![]() 2.24,
2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com