
【题目】已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)(参考数据:![]() 1.41,
1.41,![]() 1.73,
1.73,![]() 2.24,
2.24,![]() ≈2.45)
≈2.45)
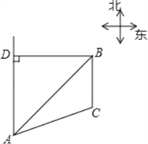
【答案】此时货轮与A观测点之间的距离AC约为15.7km.
【解析】试题分析:根据在Rt△ADB中,sin∠DAB=![]() ,得出AB的长,进而得出tan∠BAH=
,得出AB的长,进而得出tan∠BAH=![]() ,求出BH的长,即可得出AH以及CH的长,进而得出答案.
,求出BH的长,即可得出AH以及CH的长,进而得出答案.
试题解析:
BC=48×![]() =12,
=12,
在Rt△ADB中,sin∠DAB=![]() =
=![]() ,
,
∴AB=![]() =
=![]() ,
,
如图,过点B作BH⊥AC,交AC的延长线于H,
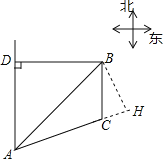
在Rt△AHB中,∠BAH=∠DAC-∠DAB=75°-45°=30°,
tan∠BAH=![]() =
=![]() ,
,
∴AH=![]() BH,
BH,
BH2+AH2=AB2,BH2+(![]() BH)2=(16
BH)2=(16![]() )2,∴BH=8
)2,∴BH=8![]() ,∴AH=8
,∴AH=8![]() ,
,
在Rt△BCH中,BH2+CH2=BC2,∴CH=4,
∴AC=AH-CH=8![]() -4≈15.7km,
-4≈15.7km,
答:此时货轮与A观测点之间的距离AC约为15.7km.


科目:初中数学 来源: 题型:
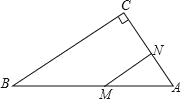
【题目】如图,在 Rt△ABC 中,∠C=90°,∠A=60°,AB=10cm,若点M 从点 B 出发以 2cm/s 的速度向点 A 运动,点 N 从点 A 出发以 1cm/s 的速度向点 C 运动,设 M、N 分别从点 B、A 同时出发,运动的时间为 ts.
(1)用含 t 的式子表示线段 AM、AN 的长;
(2)当 t 为何值时,△AMN 是以 MN 为底边的等腰三角形?
(3)当 t 为何值时,MN∥BC?并求出此时 CN 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在12×10的正方形网格中,△ABC是格点三角形,点B的坐标为(﹣5,1),点C的坐标为(﹣4,5).
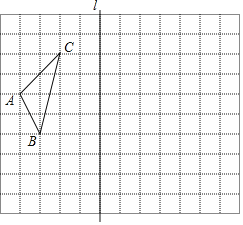
(1)请在方格纸中画出x轴、y轴,并标出原点O;
(2)画出△ABC关于直线l对称的△A1B1C1;
(3)若点P(a,b)在△ABC内,其关于直线l的对称点是P1,则P1的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
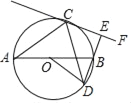
【题目】已知:如图,AB为⊙O的直径,C,D是⊙O直径AB异侧的两点,AC=DC,过点C与⊙O相切的直线CF交弦DB的延长线于点E.
(1)试判断直线DE与CF的位置关系,并说明理由;
(2)若∠A=30°,AB=4,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
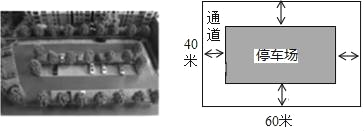
【题目】如图,城市规划部门计划在城市广场的一块长方形空地上修建乙面积为1500m2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60m,宽为40m.
(1)求通道的宽度;
(2)某公司承揽了修建停车场的工程(不考虑修通道),为了尽量减少施工对城市交通的影响,实施施工时,每天的工作效率比原计划增加了20%,结果提前2天完成任务,求该公司原计划每天修建多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解析:
由分母为![]() ,可设
,可设![]()
则![]()
![]() 对应任意x,上述等式均成立,
对应任意x,上述等式均成立,![]() ,
,![]() ,
,![]() .
.
![]() .
.
这样,分式![]() 被拆分成了一个整式
被拆分成了一个整式![]() 与一个分式
与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)当![]() 时,直接写出
时,直接写出![]() ________,
________,![]() 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式.例如:![]() ,在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像
,在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像![]() ,
,![]() ,这样的分式是假分式;像
,这样的分式是假分式;像![]() ,
,![]() ,这样的分式是真分式.类似的,假分式也可以化为整数与真分式的和的形式.
,这样的分式是真分式.类似的,假分式也可以化为整数与真分式的和的形式.
例如:![]() ;
;
![]() ;
;
或![]()
(1)分式![]() 是 分式(填“真”或“假”)
是 分式(填“真”或“假”)
(2)将分式![]() 化为整式与真分式的和的形式;
化为整式与真分式的和的形式;
(3)如果分式![]() 的值为整数,求
的值为整数,求![]() 的整数值.
的整数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com