
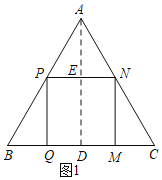
【题目】如图(1),在△ABC中,如果正方形PQMN的边QM在BC上,顶点P,N分别在AB,AC上,那么我们称这样的正方形为“三角形内接正方形”小波同学按数学家波利亚在《怎样解题》中的方法进行操作:如图(2),任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结BN′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN,小波把线段BN称为“波利亚线”,请帮助小波解决下列问题:
(1)四边形PQMN是否是△ABC的内接正方形,请证明你的结论;
(2)若△ABC为等边三角形,边长BC=6,求△ABC内接正方形的边长;
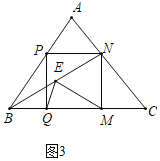
(3)如图(3),若在“波利亚线”BN上截取NE=NM,连结EQ,EM.当![]() 时,猜想∠QEM的度数,并说明你的理由.
时,猜想∠QEM的度数,并说明你的理由.

【答案】(1)四边形PQMN是△ABC的内接正方形,证明详见解析;(2)12![]() ﹣18;(3)∠QEM=90°,理由详见解析
﹣18;(3)∠QEM=90°,理由详见解析
【解析】
(1)首先证明四边形PQMN是矩形,再证明MN=PN即可;
(2)根据平行线分线段成比例定理列比例式可得结论;
(3)证明△BQE∽△BEM,推出∠BEQ=∠BME,由∠BME+∠EMN=90°,可得∠BEQ+∠NEM=90°,即可解决问题.
解:(1)四边形![]() 是
是![]() 的内接正方形,理由是:
的内接正方形,理由是:
如图2中,由画图可知![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,![]() ,
,
![]() △
△![]() ,
,
![]()
![]()
同理可得:![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形,即四边形
是正方形,即四边形![]() 是
是![]() 的内接正方形;
的内接正方形;
(2)如图1,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,设正方形
,设正方形![]() 的边长为
的边长为![]() ,
,
![]() 为等边三角形,边长
为等边三角形,边长![]() ,
,
![]() 高线
高线![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]()
![]() ,
,
即![]() ,解得:
,解得:![]() ,
,
答:![]() 内接正方形的边长是
内接正方形的边长是![]() ;
;
(3)如图3中,结论:![]() .
.
理由:设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过
经过![]() 点,直线
点,直线![]() 是抛物线的对称轴.
是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 的周长最小,求出点
的周长最小,求出点![]() 的坐标;
的坐标;
(3)若点![]() 是抛物线上一动点,当
是抛物线上一动点,当![]() 时,请直接写出点
时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子中有2枚黑棋,x枚白棋,这些棋子除颜色外无其他差别,现从盒中随机摸出一枚棋子(不放回),再随机摸出一枚棋子.
(1)若“摸出两枚棋子的颜色都是白色”是不可能事件,请写出符合条件的一个x值 ;
(2)当x=2时,“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率相等吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
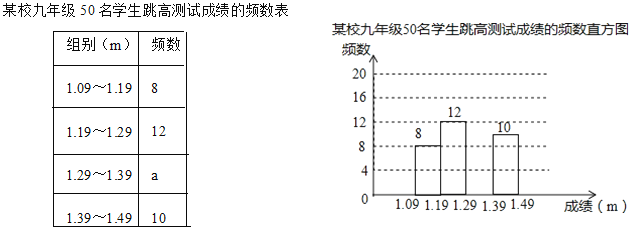
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
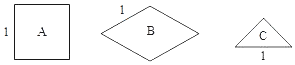
【题目】将图中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)纸片分别放在
型(等腰直角三角形)纸片分别放在![]() 个盒子中,盒子的形状、大小、质地都相同,再将这
个盒子中,盒子的形状、大小、质地都相同,再将这![]() 个盒子装入一只不透明的袋子中.
个盒子装入一只不透明的袋子中.
(1)搅匀后从中摸出![]() 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
(2)搅匀后先从中摸出![]() 个盒子(不放回),再从余下的
个盒子(不放回),再从余下的![]() 个盒子中摸出
个盒子中摸出![]() 个盒子,把摸出的
个盒子,把摸出的![]() 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形![]() 中,若
中,若![]() ,则称四边形
,则称四边形![]() 为准平行四边形.
为准平行四边形.
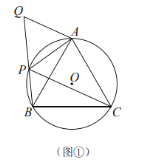
(1)如图①,![]() 是
是![]() 上的四个点,
上的四个点,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .求证:四边形
.求证:四边形![]() 是准平行四边形;
是准平行四边形;
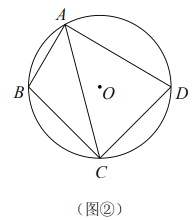
(2)如图②,准平行四边形![]() 内接于
内接于![]() ,
,![]() ,若
,若![]() 的半径为
的半径为![]() ,求
,求![]() 的长;
的长;
(3)如图③,在![]() 中,
中,![]() ,若四边形
,若四边形![]() 是准平行四边形,且
是准平行四边形,且![]() ,请直接写出
,请直接写出![]() 长的最大值.
长的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com