Question

17．已知∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC．
①若OC在∠AOB的内部，如图（1），求∠MON的度数；
②若OC在∠AOB的外部，如图（2），求∠MON的度数；
③若∠AOB=α，∠BOC=β，0°＜β＜α，α+β＜180°，其它条件不变，写出∠MON的度数．

Answer 1

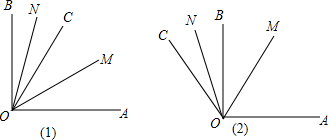
分析 ①先根据角平分线的定义得出∠MOC=$\frac{1}{2}$∠AOC，∠NOC=$\frac{1}{2}$∠BOC，再把两式相加即可得出结论；
②先根据角平分线的定义得出∠MOC=$\frac{1}{2}$∠AOC，∠NOC=$\frac{1}{2}$∠BOC，再把两式相减即可得出结论；
③根据①②的结论找出规律即可．

解答 解：①∵∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC，
∴∠MOC=$\frac{1}{2}$∠AOC，∠NOC=$\frac{1}{2}$∠BOC，
∴∠MON=∠MOC+∠NOC=$\frac{1}{2}$（∠AOC+∠BOC）=$\frac{1}{2}$∠AOB=45°；

②∵∵∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC，
∴∠MOC=$\frac{1}{2}$∠AOC，∠NOC=$\frac{1}{2}$∠BOC，
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$（∠AOC-∠BOC）=$\frac{1}{2}$∠AOB=45°；

③由①、②可知，∠MON=$\frac{1}{2}$∠AOB=$\frac{α}{2}$．

点评 本题考查的是角的计算，熟记角平分线的定义是解答此题的关键．