

分析 (1)首先利用角平分线的定义可得∠AOE的度数,由垂直的定义得∠BOF=90°,易得∠AOF,可得∠EOF;
(2)首先利用角平分线的定义可得∠AOE=$\frac{1}{2}α$,由垂直的定义得∠BOF=90°,易得∠AOF=α-90°,可得∠EOF;
(3)根据题意OB⊥OF,使得(2)中∠EOF的结果仍然成立,画出射线OF即可,再结合图形同理(2)可得结果.
解答 解:(1)∵∠AOB=130°,EO是∠AOB的平分线,
∴$∠AOE=\frac{1}{2}∠AOB=\frac{1}{2}×130°$=65°,
∵OB⊥OF,
∴∠BOF=90°,
∴∠AOF=∠AOB-∠BOF=130°-90°=40°,
∴∠EOF=∠AOE-∠AOF=65°-40°=25°;
(2)∵∠AOB=α,90°<α<180°,EO是∠AOB的平分线,
∴∠AOE=$\frac{1}{2}α$,
∵∠BOF=90°,
∴∠AOF=α-90°,
∴∠EOF=∠AOE-∠AOF=$\frac{1}{2}α$-(α-90°)=90$°-\frac{1}{2}α$;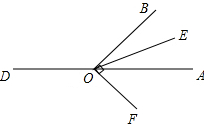
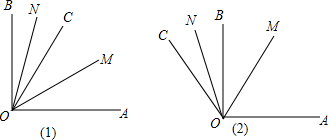
(3)如图,∵∠AOB=α,0°<α<90°,
∴∠BOE=∠AOE=$\frac{1}{2}α$,
∵∠BOF=90°,
∴∠EOF=∠BOF-∠BOE=90$°-\frac{1}{2}α$.
点评 本题主要考查了角平分线的定义和垂直的定义,结合图形利用角平分线的定义和垂直的定义是解答此题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,AB=6,G是△ABC的重心,连接AG,BG,CG
如图,△ABC中,∠ACB=90°,AB=6,G是△ABC的重心,连接AG,BG,CG查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+y=z | B. | x•y=z | C. | x+y>z | D. | x•y>z |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com