
分析 (1)根据二次根式的乘除法则运算,再合并即可求解;
(2)先把方程组变形为$\left\{\begin{array}{l}{x-7y=-4①}\\{2x+y=3②}\end{array}\right.$,再利用加简消元法求y的值,然后利用代入法求出x的值,从而得到原方程组的解;
(3)分别解两个不等式得到x<2和x≥-1,然后根据大于小的小于大的取中间的方法确定不等式组的解.
解答 解:(1)原式=$\sqrt{\frac{75}{3}}$-$\sqrt{\frac{3}{3}}$-$\sqrt{\frac{1}{5}×20}$
=5-1-2
=2;
(2)方程组变形为$\left\{\begin{array}{l}{x-7y=-4①}\\{2x+y=3②}\end{array}\right.$,
②-①×2得15y=11,
解得y=$\frac{11}{15}$,
把y=$\frac{11}{15}$代入①得x=$\frac{77}{15}$-4=$\frac{17}{15}$,
所以原方程组的解为$\left\{\begin{array}{l}{x=\frac{17}{15}}\\{y=\frac{11}{15}}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{5x-1<3(x+1)①}\\{\frac{2x-1}{3}-\frac{5x+1}{2}≤1②}\end{array}\right.$,
解①得x<2,
解②得x≥-1,
所以不等式组的解集为-1≤x<2.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解二元一次方程和一元一次不等式组.


科目:初中数学 来源: 题型:选择题
| A. | 0.65×107 | B. | 6.5×106 | C. | 65×105 | D. | 650×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
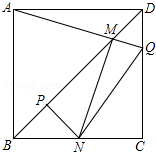 如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.
如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com