Question

8．如图，平面直角坐标系的原点O是正方形A′B′C′D′的中心，把正方形A′B′C′D′绕原点O顺时针旋转45°得正方形ABCD，且顶点A、B的坐标分别为（1，1）、（-1，1），则正方形A′B′C′D′与正方形ABCD重叠部分所形成的正八边形的周长为16$\sqrt{2}$-16．

Answer 1

分析 如图，首先求出正方形的边长、对角线长；进而求出OA′的长；证明△A′MN为等腰直角三角形，求出A′N的长度；同理求出D′M′的长度，即可解决问题．

解答 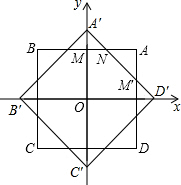解：如图，由题意得：
正方形ABCD的边长为2，
∴该正方形的对角线长为2$\sqrt{2}$，
∴OA′=$\sqrt{2}$；而OM=1，
∴A′M=$\sqrt{2}$-1；
由题意得：∠MA′N=45°，∠A′MN=90°，
∴∠MNA′=45°，
∴MN=A′M=$\sqrt{2}$-1；
由勾股定理得：A′N=2-$\sqrt{2}$；
同理可求D′M′=2-$\sqrt{2}$，
∴NM'=2-（4-2$\sqrt{2}$）=2$\sqrt{2}$-2，
∴正八边形的边长为2$\sqrt{2}$-2，
∴正八边形的周长=（2$\sqrt{2}$-2）×8=16$\sqrt{2}$-16．
故答案为：16$\sqrt{2}$-16．

点评 该题主要考查了旋转变换的性质、正方形的性质、勾股定理等几何知识点及其应用；应牢固掌握旋转变换的性质、正方形的性质等几何知识点，这是灵活运用、解题的基础和关键．