练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将下列方程化成一元方程的一般形式，并写出其中的二次项系数、一次项系数和常数项．

    ；

    ；

    ；

    ．

    【答案】见解析

    【解析】

    （1）移项得，根据二次项系数、一次项系数和常数项的定义求解即可；（2）移项得，然后根据二次项系数、一次项系数和常数项的定义求解即可；（3）原方程整理为，然后根据二次项系数、一次项系数和常数项的定义求解即可；（4）原方程整理为，然后根据二次项系数、一次项系数和常数项的定义求解即可．

    由原方程得到：，

    所以二次项系数为，一次项系数为，常数项为：；

    由原方程得到：，

    所以二次项系数为，一次项系数为，常数项为：；

    由原方程得到：，

    所以二次项系数为，一次项系数为，常数项为：；

    由原方程得到：，

    所以二次项系数为，一次项系数为，常数项为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】△ABC在平面直角坐标系中的位置如图所示．

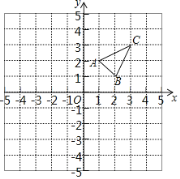
    （1）作出与△ABC关于x轴对称的△A1B1C1；

    （2）将△ABC向左平移4个单位长度，画出平移后的△A2B2C2；

    （3）若在如图的网格中存在格点P，使点P的横、纵坐标之和等于点C的横、纵坐标之和，请写出所有满足条件的格点P的坐标（C除外）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“鄂尔多斯，温暖全世界”这句广告语及上乘的质量使鄂尔多斯的羊绒制品闻名中外，我市某羊绒企业的工厂店在销售中发现：某种羊绒围巾平均每天可售出件，每件可获利元；若售价减少元，平均每天就可多售出件；若想平均每天销售这种围巾盈利元，并使顾客得到更大的实惠，那么每件围巾应降价多少元？若想获利最大，应降价多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一抛物线的顶点的坐标是，并且抛物线与轴两交点间的距离为．

    试求该抛物线的关系式；

    若点在此抛物线上，且点在第一象限，求以点、和坐标原点为顶点的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形中，，，动点、分别以、的速度从点、同时出发，点从点向点移动．

    若点从点移动到点停止，点随点的停止而停止移动，点、分别从点、同时出发，问经过多长时间、两点之间的距离是？

    若点沿着移动，点、分别从点、同时出发，点从点移动到点停止时，点随点的停止而停止移动，试探求经过多长时间的面积为？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠ABC=90°, P为射线BC上任意一点(点P和点B不重合),分别以AB,AP为边在∠ABC内部作等边△ABE和等边△APQ, 连结QE并延长交BP于点F， 若FQ=6, AB=2,则BP=__________

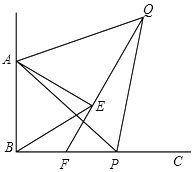
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电器超市销售A B两种型号的电风扇，A型号每台进价为200元，B型号每台进价分别为150元，下表是近两天的销售情况:

    销售时段

    销售数量

    销售收入

    A种型号

    B种型号

    第一天

    3台

    5台

    1620元

    第二天

    4台

    10台

    2760元

    (进价、售价均保持不变，利润=销售收入-进货成本)

    (1)求A、B两种型号的电风扇的销售单价;

    (2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，求A种型号的电风扇最多能采购多少台?

    (3)在(2)的条件下,超市销售完这30台电风扇能否实现利润不少于1060元的目标?若能，请给出相应的采购方案;若不能，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2017怀化，第10题，4分）如图，A，B两点在反比例函数的图象上，C，D两点在反比例函数的图象上，AC⊥y轴于点E，BD⊥y轴于点F，AC=2，BD=1，EF=3，则的值是（　　）

    A. 6 B. 4 C. 3 D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】常用的分解因式的方法有提取公因式法、公式法,但有更多的多项式只用上述方法就无法分解,如,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为：，这种分解因式的方法叫分组分解法，利用这种方法解决下列问题．

    (1)分解因式：；

    (2)△ABC三边a、b、c满足，判断△ABC的形状．

    查看答案和解析>>

    同步练习册答案