
【题目】如图,∠ABC=90°, P为射线BC上任意一点(点P和点B不重合),分别以AB,AP为边在∠ABC内部作等边△ABE和等边△APQ, 连结QE并延长交BP于点F, 若FQ=6, AB=2![]() ,则BP=__________
,则BP=__________
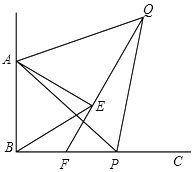
【答案】4
【解析】
连接EP,过点E作EM⊥BC,由题意可得△AQE≌△ABP,可得QE=BP,∠AEQ=∠ABC=90,可求∠EBF=∠BEF=30°,根据勾股定理可求BE=2EM=![]() ,BM=
,BM=![]() EM,EF=BF=2FM,EM=
EM,EF=BF=2FM,EM=![]() FM,可求BF=EF=2,EM=2
FM,可求BF=EF=2,EM=2![]() ,FM=1,由QF=6,EF=2,可得BP=EQ=4.
,FM=1,由QF=6,EF=2,可得BP=EQ=4.
如图,连接EP,过点E作EM⊥BC
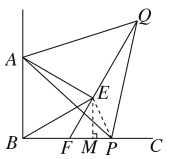
∵△AEB,△APQ是等边三角形
∴AB=AE=BE=![]() ,AQ=AP,∠ABE=∠BAE=∠QAP=60°=∠AEB
,AQ=AP,∠ABE=∠BAE=∠QAP=60°=∠AEB
∴∠BAP=∠QAE
在△ABP和△QAE中,
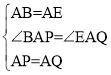
∴△ABP≌△QAE(SAS)
∴QE=BP,∠AEQ=∠ABP=90°
∵∠AEQ=∠ABC=90°,∠ABE=∠AEB=60°
∴∠BEF=∠EBF=30°
∴BF=EF,∠EFM=60°
∵EM⊥BC
∴∠FEM=30°
∴EF=2FM=BF,EM=![]() FM
FM
∵∠EBM=30°,EM⊥BC
∴BE=2EM,BM=![]() EM
EM
∵EB=2![]()
∴EM=![]() ,BM=3
,BM=3
∵BF+FM=BM
∴FM=1,BF=EF=2
∵QF=EQ+EF
∴EQ=62=4
∴BP=EQ=4
故答案为:4.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
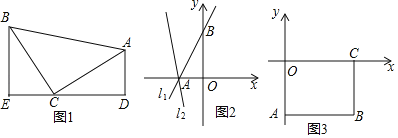
【题目】(模型建立)(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E,求证:△BEC≌△CDA.
(模型应用)(2)①已知直线l1:y=![]() x+3与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+3与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,﹣6),点A、C分别在坐标轴上,点P是线段BC上的动点,若△APD是以点D为直角顶点的等腰直角三角形,当点D在直线y=﹣2x+5上时,直接写出点D的坐标,并写出整个运动过程中点D的纵坐标n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为扩大销售增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价一元,市场每天可多售
元,为扩大销售增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价一元,市场每天可多售![]() 件,问他降价多少元时,才能使每天所赚的利润最大?并求出最大利润.
件,问他降价多少元时,才能使每天所赚的利润最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的边长为1,点B、C的坐标分别为(-1, 3), (0, 1).
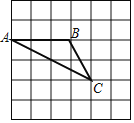
(1)建立符合条件的直角坐标系(要求标出x轴,y轴和原点),并写出点A的坐标
(2)线段AB上任意一点的坐标可以表示为
(3)在y轴上找到一点P,使得S△ABP = 3S△ABC,求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com