
【题目】已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
, ![]() 与
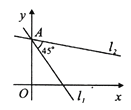
与![]() 在A点相交所形的 夹角为45°(如图所示),则直线
在A点相交所形的 夹角为45°(如图所示),则直线![]() 的函数表达式为____________.
的函数表达式为____________.
【答案】y=![]() x+2
x+2
【解析】
由题意得A(0,2),B(1,0),作BD⊥AB交直线12于D,作DC⊥x轴于C,利用全等三角形的性质求出点D坐标,再运用待定系数法即可解答.
解:
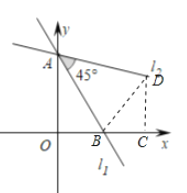
解:如图:作BD⊥AB交直线l2于D,作DC⊥x轴于C,
由题意得A(0,2),B(1,0)
∵∠DAB=45°
∴∠ADB=45°,
∴BD=AB
∵∠DCB=∠ABD=∠AOB=90°
∴∠DBC+ ∠CDB=90°,∠DBC+∠ABO=90°
∴∠CDB=∠ABO,
∴△DCB≌△BOA(AAS),
∴DC=OB=1,BC=OA=2
∴D(3,1)
设直线12的解析式为y=kx+b,则
![]() 解得
解得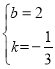
∴直线l2的函数表达式为y=![]() x+2
x+2
故答案为y=![]() x+2
x+2


科目:初中数学 来源: 题型:
【题目】如图,∠ABC=90°, P为射线BC上任意一点(点P和点B不重合),分别以AB,AP为边在∠ABC内部作等边△ABE和等边△APQ, 连结QE并延长交BP于点F, 若FQ=6, AB=2![]() ,则BP=__________
,则BP=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点 B、O分别落在点 B1、C1 处,点B1在x轴上,再将△AB1C1 绕点 B1 顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2 绕点C2 顺时针旋转到△A2B2C2 的位置,点 A2 在x轴上,依次进行下去….若点 A(![]() ,0),B(0,4),则点 B2016 的横坐标为_______.
,0),B(0,4),则点 B2016 的横坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数![]() 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】常用的分解因式的方法有提取公因式法、公式法,但有更多的多项式只用上述方法就无法分解,如![]() ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为:
,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为:![]() ,这种分解因式的方法叫分组分解法,利用这种方法解决下列问题.
,这种分解因式的方法叫分组分解法,利用这种方法解决下列问题.
(1)分解因式:![]() ;
;
(2)△ABC三边a、b、c满足![]() ,判断△ABC的形状.
,判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
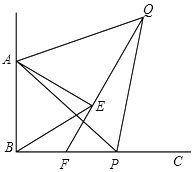
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的是
BF;④AE=BG.其中正确的是

A. ①② B. ①③ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.
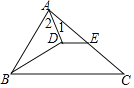
(1)求证:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某河道上有一个半圆形的拱桥,河两岸筑有拦水堤坝.其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线![]() 、
、![]() 与半圆相切,上、下桥斜面的坡度
与半圆相切,上、下桥斜面的坡度![]() ,桥下水深
,桥下水深![]() 米.水面宽度
米.水面宽度![]() 米.设半圆的圆心为
米.设半圆的圆心为![]() ,直径
,直径![]() 在坡角顶点
在坡角顶点![]() 、
、![]() 的连线上.求从
的连线上.求从![]() 点上坡、过桥、下坡到
点上坡、过桥、下坡到![]() 点的最短路径长.(参考数据:
点的最短路径长.(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在平面直角坐标系中,A,B,D 三点的坐标是(0,2),(-2,0),(1,0),点C 是 x 轴下方一点,且 CD⊥AD,∠BAD+∠BCD=180°,AD=CD

(1)求证:BD 平分∠ABC
(2)求四边形 ABCD 的面积
(3)如图 2,BE 是∠ABO 的邻补角的平分线,连接 AE,OE 交 AB 于点 F,若∠AEO=45°,求证:AF=AO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com