
【题目】如图 1,在平面直角坐标系中,A,B,D 三点的坐标是(0,2),(-2,0),(1,0),点C 是 x 轴下方一点,且 CD⊥AD,∠BAD+∠BCD=180°,AD=CD

(1)求证:BD 平分∠ABC
(2)求四边形 ABCD 的面积
(3)如图 2,BE 是∠ABO 的邻补角的平分线,连接 AE,OE 交 AB 于点 F,若∠AEO=45°,求证:AF=AO.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析;
;(3)证明见解析;
【解析】
(1)过C作DM⊥BD于M,根据AAS判定△CDM≌△DOA,通过线段和差推出BM=MC=1得出∠CBD=45°进而得到∠CBD=∠ABO=45°即可证BD 平分∠ABC;
(2)将![]() ,再根据三角形的面积公式计算即可;
,再根据三角形的面积公式计算即可;
(3)过点E作作EH⊥x轴于点H,EG⊥BC于点G,根据角平分线的性质得到EH=EG,证明△EAG≌△EOH,得到EA=EO,根据等腰三角形的判定定理解答.
证明:(1)∵A(0,2)B(-2,0)D(1,0)
∴OA=OB=2,OD=1
∴∠ABO=∠BAO=45°
过C作DM⊥BD于M
∴∠CMD=90°
∴∠1+∠3=90°
∵CD⊥AD
∴∠ADC=90°
∴∠1+∠2=90°
∴∠2=∠3
又∵CD=AD,∠CMD=∠AOD =90°
∴△CDM≌△DOA
∴CM=OD=1,MD=AO=2
∴OM=1
∴BM=1
∴BM=MC=1
∴∠CBD=45°
∴∠CBD=∠ABO=45°
∴BD 平分∠ABC
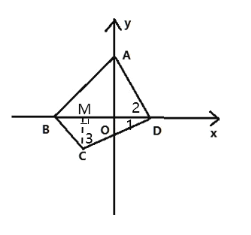
(2)由(1)得A(0,2),B(-2,0),C(-1,-1),M(-1,0)
∴BD=3,AO=2,CM=1
∴![]()
∴![]()
(3)过点E作EH⊥x轴于点H,EG⊥BA于点G,
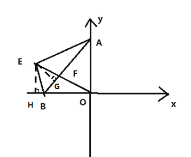
∴∠EHO=∠EGA =90°
∵E点在∠ABO的邻补角的平分线上,EH⊥HO,EG⊥BA
∴EH=EG,
∵∠ABO=∠AEO=45,
∴∠EAG=∠EOH,
在△EAG和EOH中,
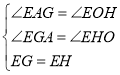
∴△EAG≌△EOH(AAS),
∴EA=EO,
∵∠AEO=45°,
∴∠EAO=∠EOA=67.5°,
∵∠OAB=45°,
∴∠AFO=180°-∠OAB-∠AOE=67.5°
∴∠AOE=∠AFO=67.5°,
∴AF=AO


科目:初中数学 来源: 题型:
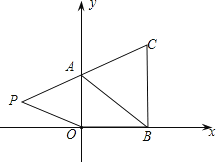
【题目】如图,在下面直角坐标系中,已知![]() ,
,![]() ,
,![]() 三点,其中
三点,其中![]() 、
、![]() 、
、![]() 满足关系式
满足关系式![]() ,
,![]() .
.
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)如果在第二象限内有一点![]() ,请用含
,请用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(3)在(2)的条件下,是否存在点![]() ,使四边形
,使四边形![]() 的面积与
的面积与![]() 的面积相等?若存在,求出点
的面积相等?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
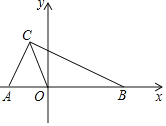
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|a+2|+(b﹣4)2=0
(1)求a,b的值;
(2)在y轴上是否存在一点M,使△COM的面积=![]() △ABC的面积,求出点M的坐标.
△ABC的面积,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,点 D,E 分别在∠ABC 和∠ACB 的平分线上,连接 BD,DE,EC,若∠D+∠E=295°, 则∠A 是( )
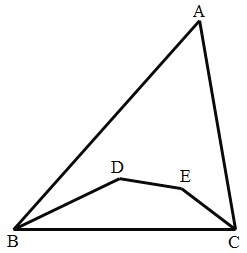
A.65°B.60°C.55°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校八年级学生数学学习情况,随机抽查该年级若干名学生进行测试,然后把测试结果分为4个等级:A、B、C、D,并将统计结果绘制成两幅不完整的统计图,请根据图中的信息解答下列问题
(1)补全条形统计图
(2)等级为D等的所在扇形的圆心角是 度
(3)如果八年级共有学生1800名,请你估算我校学生中数学学习A等和B等共多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
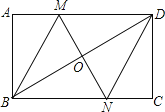
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
![]() 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形;
![]() 若
若![]() ,
,![]() ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线分别交BC,CD于E、F.
(1)试说明△CEF是等腰三角形.
(2)若点E恰好在线段AB的垂直平分线上,试说明线段AC与线段AB之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,与
与x轴交于点A,B,与![]() 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。

(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com