
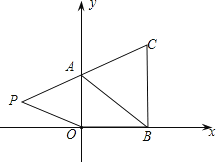
【题目】如图,在下面直角坐标系中,已知![]() ,
,![]() ,
,![]() 三点,其中
三点,其中![]() 、
、![]() 、
、![]() 满足关系式
满足关系式![]() ,
,![]() .
.
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)如果在第二象限内有一点![]() ,请用含
,请用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(3)在(2)的条件下,是否存在点![]() ,使四边形
,使四边形![]() 的面积与
的面积与![]() 的面积相等?若存在,求出点
的面积相等?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)a=2,b=3,c=4;(2)-m+3;(3)P(-3,![]() )
)
【解析】
(1)根据二次根式和平方的非负性可得结论;
(2)根据P和A、B的坐标,由S四边形ABOP=S△AOP+S△AOB可得结论;
(3)根据四边形ABOP的面积与△ABC的面积相等,列式可得m=-3,从而得P的坐标.
解:(1)∵+(b-3)2=0,(c-4)2≤0,
∴a-2=0,b-3=0,c-4=0,
∴a=2,b=3,c=4;
(2)由(1)知:OA=2,OB=3,
∴S四边形ABOP=S△AOP+S△AOB=![]() AO|xP|+
AO|xP|+![]() AOOB=-m+
AOOB=-m+![]() =-m+3;
=-m+3;
(3)∵B(3,0),C(3,4),
∴BC⊥x轴,
∴S△ABC=![]() BCxB=
BCxB=![]() ×4×3=6,
×4×3=6,
∴-m+3=6,
m=-3,
则当m=-3时,四边形ABOP的面积与△ABC的面积相等,此时P(-3,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点 B、O分别落在点 B1、C1 处,点B1在x轴上,再将△AB1C1 绕点 B1 顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2 绕点C2 顺时针旋转到△A2B2C2 的位置,点 A2 在x轴上,依次进行下去….若点 A(![]() ,0),B(0,4),则点 B2016 的横坐标为_______.
,0),B(0,4),则点 B2016 的横坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.
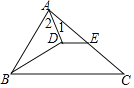
(1)求证:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某河道上有一个半圆形的拱桥,河两岸筑有拦水堤坝.其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线![]() 、
、![]() 与半圆相切,上、下桥斜面的坡度
与半圆相切,上、下桥斜面的坡度![]() ,桥下水深
,桥下水深![]() 米.水面宽度
米.水面宽度![]() 米.设半圆的圆心为
米.设半圆的圆心为![]() ,直径
,直径![]() 在坡角顶点
在坡角顶点![]() 、
、![]() 的连线上.求从
的连线上.求从![]() 点上坡、过桥、下坡到
点上坡、过桥、下坡到![]() 点的最短路径长.(参考数据:
点的最短路径长.(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一根长![]() 的铁丝分为两段,并把每一段都弯成一个正方形,设其中一个正方形的边长为
的铁丝分为两段,并把每一段都弯成一个正方形,设其中一个正方形的边长为![]() ,则另一个正方形的边长为________
,则另一个正方形的边长为________![]() ,设这两个正方形的面积的和为
,设这两个正方形的面积的和为![]() ,则
,则![]() 与
与![]() 之间的函数关系式为________;当两个正方形的边长分别为________、________时,
之间的函数关系式为________;当两个正方形的边长分别为________、________时,![]() 有最小值,最小值是________
有最小值,最小值是________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能够判别一个四边形是菱形的条件是( )
A. 一组对角相等且一条对角线平分这组对角 B. 对角线互相平分
C. 对角线互相垂直且相等 D. 对角线相等且互相平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在平面直角坐标系中,A,B,D 三点的坐标是(0,2),(-2,0),(1,0),点C 是 x 轴下方一点,且 CD⊥AD,∠BAD+∠BCD=180°,AD=CD

(1)求证:BD 平分∠ABC
(2)求四边形 ABCD 的面积
(3)如图 2,BE 是∠ABO 的邻补角的平分线,连接 AE,OE 交 AB 于点 F,若∠AEO=45°,求证:AF=AO.
查看答案和解析>>
科目:初中数学 来源: 题型:
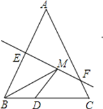
【题目】如图,等腰△ABC的底边BC的长为2cm,面积是6cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为____________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com