
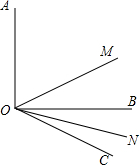
 (1)如图所示,OM平分∠AOC,ON平分∠BOA
(1)如图所示,OM平分∠AOC,ON平分∠BOA分析 (1)根据角平分线的定义得到∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC,则∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB,然后把∠AOB的度数代入计算即可;
(2)根据题意列方程解答即可.
解答 解:(1)①∵∠AOB=90°,∠BOC=30°,
∴∠AOC=120°,
∵OM平分∠AOC,ON平分∠BOA,
∴∠MOC=$\frac{1}{2}$∠AOC=60°,∠CON=$\frac{1}{2}$∠BOC=15°,
∴∠MON=∠MOC-∠CON=45°;
②∵∠AOB=80°,∠BOC=30°,
∴∠AOC=110°,
∵OM平分∠AOC,ON平分∠BOA,
∴∠MOC=$\frac{1}{2}$∠AOC=55°,∠CON=$\frac{1}{2}$∠BOC=15°,
∴∠MON=∠MOC-∠CON=40°;
③∵∠AOB=m°,∠BOC=n°,
∴∠AOC=(m+n)°,
∵OM平分∠AOC,ON平分∠BOA,
∴∠MOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(m+n)°,∠CON=$\frac{1}{2}$∠BOC=$\frac{1}{2}$n°,
∴∠MON=∠MOC-∠CON=$\frac{1}{2}$m°.
故答案为:45°,40°,$\frac{1}{2}$m;
(2)当$|\begin{array}{l}{2}&{-4}\\{(x-1)}&{5}\end{array}|$=18时,
∴2×5-[(-4)×(x-1)]=18,
解得:x=3.
点评 本题考查了角的计算,解一元一次方程,角平分线的定义,属于基础题.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | B. | $\sqrt{1{6}^{2}+{9}^{2}}$=16+9=25 | ||
| C. | 2$\sqrt{2}$+3$\sqrt{2}$=5$\sqrt{2}$ | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
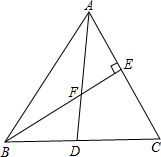 如图,锐角△ABC中.AD是∠BAC的平分线.线段BE垂直AC于E点.交线段AD于F.
如图,锐角△ABC中.AD是∠BAC的平分线.线段BE垂直AC于E点.交线段AD于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com