
【题目】已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.
(1)请你添加一个适当的条件 ,使得四边形ABCD是平行四边形,并证明你的结论;
(2)作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(3)在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=![]() ,求⊙O的半径.
,求⊙O的半径.
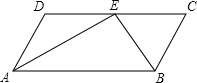
【答案】(1)当AD=BC时,四边形ABCD是平行四边形,理由见解析;(2)作出相应的图形见解析;(3)圆O的半径为2.5.
【解析】(1)添加条件AD=BC,利用一组对边平行且相等的四边形为平行四边形验证即可;
(2)作出相应的图形,如图所示;
(3)由平行四边形的对边平行得到AD与BC平行,可得同旁内角互补,再由AE与BE为角平分线,可得出AE与BE垂直,利用直径所对的圆周角为直角,得到AF与FB垂直,可得出两锐角互余,根据角平分线性质及等量代换得到∠AGF=∠AEB,根据sin∠AGF的值,确定出sin∠AEB的值,求出AB的长,即可确定出圆的半径.
(1)当AD=BC时,四边形ABCD是平行四边形,理由为:
证明:∵AD∥BC,AD=BC,
∴四边形ABCD为平行四边形;
故答案为:AD=BC;
(2)作出相应的图形,如图所示;
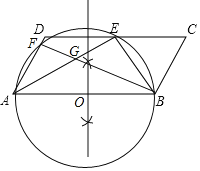
(3)∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵AE与BE分别为∠DAB与∠CBA的平分线,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∵AB为圆O的直径,点F在圆O上,
∴∠AFB=90°,
∴∠FAG+∠FGA=90°,
∵AE平分∠DAB,
∴∠FAG=∠EAB,
∴∠AGF=∠ABE,
∴sin∠ABE=sin∠AGF=![]() ,
,
∵AE=4,
∴AB=5,
则圆O的半径为2.5.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
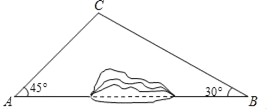
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
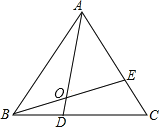
【题目】如图,点D、E分别是等边三角形ABC的边BC、AC上的点,连接AD、BE交于点O,且△ABD≌△BCE.
(1)若AB=3,AE=2,则BD= ;
(2)若∠CBE=15°,则∠AOE= ;
(3)若∠BAD=a,猜想∠AOE的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
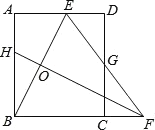
【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50度.
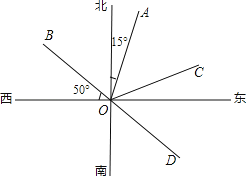
(1)若∠AOC=∠AOB,则OC的方向是 ;
(2)OD是OB的反向延长线,OD的方向是 ;
(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是 ;
(4)在(1)、(2)、(3)的条件下,∠COE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上.
①如图1,若∠BCA=90°,∠α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 ,使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为 1 的小正方形组成的网格中,有如图 所示的 A. B 两点,在格点中任 意放置点 C,恰好能使△ABC 的面积为 1,则这样的 C 点有 ( )个
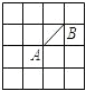
A. 5 个B. 6 个C. 7 个D. 8 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com