
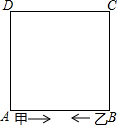
 如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.
如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.分析 (1)由于两人不是在同一顶点出发,所以两人第一次在同一顶点相遇,需要通过的距离之和等于周长的整数倍再加一条边的长度,即85t=40n+10,其中n是第一次在同一顶点相遇之前通过的周长的个数;
(2)设甲走x米,则乙走$\frac{30}{55}$x=$\frac{6}{11}$x米,由于相遇在正方形顶点,所以x和$\frac{6}{11}$x都要为10的整数倍且x+$\frac{6}{11}$x-10=$\frac{17}{11}$x-10,为40的整数倍,根据(a-$\frac{10}{85}$)×85=40(b-1)+20,即可求解.
解答 解:(1)∵两个人的速度之和是85米每分钟,$\frac{10}{85}$分钟后两人第一次相遇.如果要两人在顶点相遇,
则:每个人所走的路程均为10的整数倍,且两个人所走路程之和为10+40n(n是指边的条数).
S=10+40n,n为0、1、2、3…n ①
S甲=55t,可以被10整除,t为2、4、6…②
S乙=30t,也可以被10整除,t为甲方取值即可,
∵S=S甲+S乙,
整理得:55t+30t=10+40n,即:85t=10+40n,
∴n=$\frac{85t-10}{40}$③,
由①②③得:当t=2时,两人第一次在顶点相遇.
此时甲走了110米,乙走了60米,相遇在点D.
(2)甲、乙相遇则两者走的时间相同,
设甲走x米,则乙走$\frac{30}{55}$x=$\frac{6}{11}$x米,
∵要相遇在正方形顶点,
∴x和$\frac{6}{11}$x都要为10的整数倍且x+$\frac{6}{11}$x-10=$\frac{17}{11}$x-10,为40的整数倍(除第一次走10米相遇,以后每次相遇都要再走40米),
∴(a-$\frac{10}{85}$)×85=40(b-1)+20,
由上式可知:当a=6时,甲走了330米,甲走到点B,
乙走了180米,乙走到点D,
解得:b=13,
故答案为:2,(6,13).
点评 本题考查了一元一次方程在行程问题中的应用,解题的难点在于,如果用经典的数学演绎推理,容易将此题化归为“不定方程”这一学生没有系统学习过的数学模型.所以,没有用合情推理研究本题,是解答此题的一个解题策略层面的方向性错误.学生是否有合理运用“合情推理”的意识,是否知道在怎样的情况下要用合情推理,在怎样的情况下不宜用合情推理,这是学生能否正确选择这道题的解题策略方向的关键所在.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
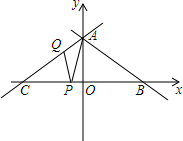 如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.
如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-2x+4=0 | B. | x2-2x-1=0 | C. | 2x2-2x-5=0 | D. | x2+2x-1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{πx}{5}$的系数是$\frac{1}{5}$ | B. | $\frac{3x-1}{3}$是单项式 | ||
| C. | -25m是5次单项式 | D. | -x2y-35xy3是四次多项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com