
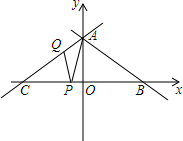
 如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.
如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.分析 (1)由B点是直线AB与x轴的交点,故令y=0,解出x的值即为B点的坐标,A点是直线AB与y轴的交点,令x=0,可得出A点坐标,由三角函数的正弦值可得出∠ABC的值;(2)圆与直线相切,圆的半径就等于圆心到直线的距离,结合点到直线的距离公式即可得出结论;(3)由两个等于30°的角和一个公共角可得出△CAP∽△PAQ,根据相似三角形的性质可找出AQ的值,再由CQ=AC-AQ,即可得出结论;(4)若三角形为等腰三角形,只需两条边相等即可,在此分哪两条边相等来讨论,即可得出结论.
解答 解:(1)令y=0,则有0=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$,
解得:x=8.
即点B的坐标是(8,0).
令x=0,则有y=$\frac{8\sqrt{3}}{3}$,
即点A的坐标为(0,$\frac{8\sqrt{3}}{3}$).
∴AO=$\frac{8\sqrt{3}}{3}$,BO=8,
∴tan∠ABO=$\frac{AO}{BO}$=$\frac{\sqrt{3}}{3}$,
∴∠ABO=30°.
故答案为:(8,0);30.
(2)∵⊙O与AB相切,
∴⊙O的半径为点O到直线AB的距离.
直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$可变形为$\frac{\sqrt{3}}{3}$x+y-$\frac{8\sqrt{3}}{3}$=0.
点O到直线AB的距离=$\frac{|0+0-\frac{8\sqrt{3}}{3}|}{\sqrt{(\frac{\sqrt{3}}{3})^{2}+{1}^{2}}}$=4.
∴⊙O的半径为4.
故答案为:4.
(3)∵直线AC与AB关于y轴对称,
∴点C坐标为(-8,0),∠ACB=∠ABC=30°.
又∵点A的坐标为(0,$\frac{8\sqrt{3}}{3}$),点P的坐标为(-2,0),
∴AO=$\frac{8\sqrt{3}}{3}$,CO=8,AC=$\sqrt{A{O}^{2}+C{O}^{2}}$=$\frac{16\sqrt{3}}{3}$,PO=2,CP=CO-PO=6,AP=$\sqrt{A{O}^{2}+P{O}^{2}}$=$\frac{2\sqrt{57}}{3}$.
∵∠CAP=∠PAQ,∠ACP=∠APQ=30°,
∴△CAP∽△PAQ,
∴$\frac{AQ}{AP}$=$\frac{AP}{AC}$,AQ=$\frac{A{P}^{2}}{AC}$=$\frac{19\sqrt{3}}{12}$.
CQ=AC-AQ=$\frac{15\sqrt{3}}{4}$.
故当P点坐标为(-2,0)时,CQ的长为$\frac{15\sqrt{3}}{4}$.
(4)△APQ为等腰三角形分三种情况:
①当AQ=PQ时,如图1,
∵∠APQ=30°,AQ=PQ,
∴∠PAQ=30°,
∵∠ACO=30°,∠CAO=90°-∠ACO=60°,
∴∠PAO=∠CAO-∠PAQ=30°.
∵AO⊥BC,
∴PO=AO•tan∠PAO=$\frac{8}{3}$,
∴点P的坐标为(-$\frac{8}{3}$,0).
②当AP=AQ时,如图2,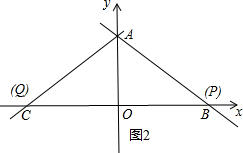
此时P点与B点重合,Q点与C点重合,
∴点P的坐标为(8,0).
③当AP=PQ时,如图3,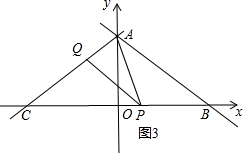
∵∠APQ=30°,∠PAQ=∠PQA=$\frac{(180°-30°)}{2}$=75°,
∴∠CPA=180°-∠ACP-CAP=180°-30°-75°=75°,
∴∠CAP=∠CPA=75°,
∴CP=CA=$\frac{16\sqrt{3}}{3}$,
OP=CP-CO=$\frac{16\sqrt{3}}{3}$-8.
∴点P的坐标为($\frac{16\sqrt{3}}{3}$-8,0).
综上可知:当△APQ为等腰三角形时,P点的坐标为(8,0)或(-$\frac{8}{3}$,0)或($\frac{16\sqrt{3}}{3}$-8,0).
点评 本题以一次函数的综合应用为背景考查了一次函数图象与坐标轴的交点、相似三角形的判定及性质、特殊角的三角函数值以及等腰三角形的判定,解题的关键是:(1)会求直线与坐标轴的交点问题以及知道特殊角的三角函数值;(2)明白圆与直线相切,半径等于圆心到直线的距离;(3)能发现相似三角形,会用相似三角形的判定及性质解决问题;(4)知道等腰三角形的性质.本题属于中等难度题,易出现错误的地方在(4)中,会落下当AP=AQ时这种情况.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
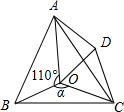 如图,点O是等边三角形ABC内一点,将△BOC绕点C顺时针方向旋转60°得到△ADC,连接OD,已知∠AOB=110°.
如图,点O是等边三角形ABC内一点,将△BOC绕点C顺时针方向旋转60°得到△ADC,连接OD,已知∠AOB=110°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
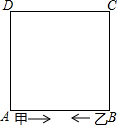 如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.
如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com