
【题目】如图,AB切⊙O于点B,BC∥OA,交⊙O于点C,若∠OAB=30°,BC=6,则劣弧BC的长为 . 
【答案】2π
【解析】解:连接OB,OC,
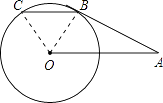
∵AB为圆O的切线,
∴∠ABO=90°,
在Rt△ABO中,∠OAB=30°,
∴∠AOB=60°,
∵BC∥OA,
∴∠OBC=∠AOB=60°,
又∵OB=OC,
∴△BOC为等边三角形,
∴∠BOC=60°,BO=CO=BC=6,
则劣弧BC长= ![]() =2π.
=2π.
答案为:2π.
【考点精析】本题主要考查了切线的性质定理和弧长计算公式的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】为了解我校七年级![]() 名学生的体重情况,现从中随机抽取
名学生的体重情况,现从中随机抽取![]() 名学生测量体重进行统计分析,关于本次调查下列说法正确的是( )
名学生测量体重进行统计分析,关于本次调查下列说法正确的是( )
A.本次调查中的总体是七年级![]() 名学生
名学生
B.本次调查中的样本是随机抽取的![]() 名学生的体重
名学生的体重
C.本次调查中的样本容量是![]() 名
名
D.本次调查中的个体是七年级的每个学生
查看答案和解析>>
科目:初中数学 来源: 题型:
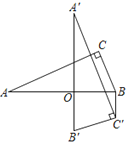
【题目】如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕AB上的点O顺时针旋转90°,得到△A'B'C',连结BC'.若BC'∥A'B',则OB的值为( )
A. ![]() B. 5C.
B. 5C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
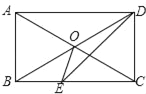
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
一般的,如果一个正数x的平方等于a,即x2=a,那么正数x就叫做a的算术平分根,记作![]() (即
(即![]() ),如
),如![]() ,3就叫做9的算术平方根.
,3就叫做9的算术平方根.
(1)计算下列各式的值:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)观察(1)中的结果,![]() ,
,![]() ,
,![]() 这三个数之间存在什么关系?________________________
这三个数之间存在什么关系?________________________
(3)由(2)得出的结论猜想:![]() ________(
________(![]() ,
,![]() );
);
(4)根据(3)计算:![]() ________,
________,![]() ________,
________,![]() =________(写最终结果)
=________(写最终结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商城销售![]() 、
、![]() 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为![]() 元、
元、![]() 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:
销售时段 | 销售型号 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 、
、![]() 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;
(2)若商城准备用不多于![]() 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共![]() 台,求
台,求![]() 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?
(3)在(2)的条件下商城销售完这![]() 台电风能否实现利润超过
台电风能否实现利润超过![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.

(1)求证:四边形ABCD是菱形;
(2)如果两张矩形纸片的长都是8,宽都是2.那么△DCB的面积是否存在最大值或最小值?如果存在,请求出来;如果不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com