
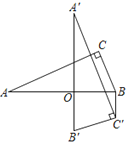
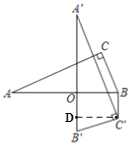
【题目】如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕AB上的点O顺时针旋转90°,得到△A'B'C',连结BC'.若BC'∥A'B',则OB的值为( )
A. ![]() B. 5C.
B. 5C. ![]() D.
D. ![]()
【答案】A
【解析】
过C′作C′D⊥A′B′于D,可得∠A′DC′=90°,由旋转性质可得∠BOD=90°,进而可证明AB//C′D,由BC′//A′B′,可证明四边形ODC′B是矩形,可得OB=C′D,由勾股定理可求出AB的长,利用面积公式求出C′D的长即可得答案.
过C′作C′D⊥A′B′于D,
∴∠A′DC′=90°,
∵将△ABC绕AB上的点O顺时针旋转90°,得到△A'B'C',
∴∠BOD=90°,
∴AB//C′D,
∵BC′//A′B′,
∴四边形ODC′B是矩形,
∴OB=C′D,
∵∠C=90°,AC=12,BC=5,
∴AB=![]() =13,
=13,
∵S△A′B′C′=![]() A′B′
A′B′![]() C′D=
C′D=![]() B′C′
B′C′![]() A′C′,
A′C′,
∴C′D=![]() =
=![]() =
=![]() ,
,
∴OB=C′D=![]() ,
,
故选A.


科目:初中数学 来源: 题型:
【题目】已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A= ![]() .(注:不要求写作法,但保留作图痕迹)
.(注:不要求写作法,但保留作图痕迹)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
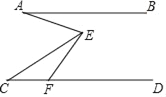
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是数轴上的两点,
是数轴上的两点,![]() 为原点,点
为原点,点![]() 表示的数是1,点
表示的数是1,点![]() 在点
在点![]() 的左侧,
的左侧,![]() .
.
![]()
(1)求点![]() 表示的数;
表示的数;
(2)数轴上的一点![]() 在点
在点![]() 的右侧,设点
的右侧,设点![]() 表示的数是
表示的数是![]() ,若点
,若点![]() 到
到![]() ,
,![]() 两点的距离的和是15,求
两点的距离的和是15,求![]() 的值;
的值;
(3)动点![]() 从
从![]() 点出发,以每秒2个单位的速度向右运动,同时动点
点出发,以每秒2个单位的速度向右运动,同时动点![]() 从
从![]() 点出发,以每秒1个单位的速度向右运动,设运动时间为
点出发,以每秒1个单位的速度向右运动,设运动时间为![]() 秒,是否存在这样的
秒,是否存在这样的![]() 值,使
值,使![]() ,若存在,请求出
,若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,第n次操作后,得到△AnBnCn,要使△AnBnCn的面积超过2020,则至少需要操作__________次.

查看答案和解析>>
科目:初中数学 来源: 题型:
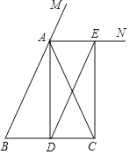
【题目】已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )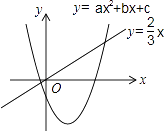
A.大于0
B.等于0
C.小于0
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com