
【题目】已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A= ![]() .(注:不要求写作法,但保留作图痕迹)
.(注:不要求写作法,但保留作图痕迹)![]()
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 为
为![]() 轴上的动点,点
轴上的动点,点![]() 为
为![]() 轴上方的动点,连接
轴上方的动点,连接![]() ,
,![]() ,
,![]() .
.
(1)如图1,当点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() 的角平分线与
的角平分线与![]() 的角平分线交于点
的角平分线交于点![]() ,请直接写出
,请直接写出![]() 的度数;
的度数;

(2)如图2,当点![]() 在
在![]() 轴上,
轴上,![]() 的角平分线与
的角平分线与![]() 的角平分线交于点
的角平分线交于点![]() ,点
,点![]() 在
在![]() 的延长线上,且满足
的延长线上,且满足![]() ,求
,求![]() ;
;

(3)如图3,当点![]() 在第一象限内,点
在第一象限内,点![]() 是
是![]() 内一点,点
内一点,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上一点,满足:
上一点,满足:![]() ,
,![]() ,
,![]() .
.

以下结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() .
.
正确的是:________.(请填写正确结论序号,并选择一个正确的结论证明,简写证明过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空

如图,因为∠A=_____(已知),
所以AC∥ED( )
因为∠2=_____(已知),
所以AC∥ED( )
因为∠A+_____=180°(已知),
所以AB∥FD( )
因为AB∥_____(已知),
所以∠2+∠AED=180°( )
因为AC∥_____(已知),
所以∠C=∠3( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2017年“KFC”篮球赛进校园活动中,某校甲、乙两队进行决赛,比赛规则规定:两队之间进行3局比赛,3局比赛必须全部打完,只要赢满2局的队为获胜队,假如甲、乙两队之间每局比赛输赢的机会相同,且乙队已经赢得了第1局比赛,那么甲队获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中;长方形ABCD的四个顶点分别为
中;长方形ABCD的四个顶点分别为![]() ;
;![]() ,
,![]() ,
,![]() .对该长方形及其内部的每一个点都进行如下操作:把每个点的横坐标都乘以同一个实数
.对该长方形及其内部的每一个点都进行如下操作:把每个点的横坐标都乘以同一个实数![]() ,纵坐标都乘以3,再将得到的点向右平移
,纵坐标都乘以3,再将得到的点向右平移![]() 个单位,向下平移
个单位,向下平移![]() 个单位,得到长方形
个单位,得到长方形![]() 及其内部的点,其中点
及其内部的点,其中点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点分别为A’,B’,C’,D’,
的对应点分别为A’,B’,C’,D’,
(1)点A’的横坐标为______(用含![]() ,
,![]() 的式子表示)
的式子表示)
(2)若点A’的坐标为![]() ,点C’的坐标为
,点C’的坐标为![]() ,求
,求![]() ,
,![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为( )
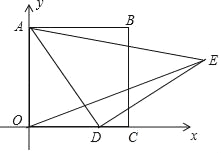
A. ![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我校七年级![]() 名学生的体重情况,现从中随机抽取
名学生的体重情况,现从中随机抽取![]() 名学生测量体重进行统计分析,关于本次调查下列说法正确的是( )
名学生测量体重进行统计分析,关于本次调查下列说法正确的是( )
A.本次调查中的总体是七年级![]() 名学生
名学生
B.本次调查中的样本是随机抽取的![]() 名学生的体重
名学生的体重
C.本次调查中的样本容量是![]() 名
名
D.本次调查中的个体是七年级的每个学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕AB上的点O顺时针旋转90°,得到△A'B'C',连结BC'.若BC'∥A'B',则OB的值为( )
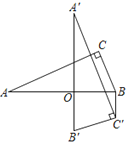
A. ![]() B. 5C.
B. 5C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com