
【题目】如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长.

【答案】6
【解析】
作DE⊥BC,交BC延长线于E,如图,则四边形BEDP为矩形,再利用等角的余角相等得到∠ADP=∠CDE,则可利用“AAS”证明△ADP≌△CDE,得到DP=DE,S△ADP=S△CDE,所以四边形BEDP为正方形,S四边形ABCD=S矩形BEDP,根据正方形的面积公式得到DP2=36,易得DP=6.
解:作DE⊥BC,交BC延长线于E,如图,∵DP⊥AB,ABC=90°,∴四边形BEDP为矩形,∴∠PDE=90°,即∠CDE+∠PDC=90°.
∵∠ADC=90°,即∠ADP+∠PDC=90°,∴∠ADP=∠CDE.在△ADP和△CDE中, ,∴△ADP≌△CDE,∴DP=DE,S△ADP=S△CDE,∴四边形BEDP为正方形,S四边形ABCD=S矩形BEDP,∴DP2=36,∴DP=6.
,∴△ADP≌△CDE,∴DP=DE,S△ADP=S△CDE,∴四边形BEDP为正方形,S四边形ABCD=S矩形BEDP,∴DP2=36,∴DP=6.



科目:初中数学 来源: 题型:
【题目】如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )

A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲,乙两种服装后,都加价50%标价出售.春节期间,商场搞优惠促销,决定将甲,乙两种服装分别按标价的七折和八折出售.某顾客购买甲,乙两种服装共付款186元,两种服装标价和为240元.问:这两种服装打折之后售出的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八(1)班同学为了解2018年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:


(1)本次调查采用的调查方式是________(填“普查”或“抽样调查”),样本容量是________;
(2)补全频数分布直方图:
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“![]() ”的圆心角度数是________;
”的圆心角度数是________;
(4)若该小区有5000户家庭,求该小区月均用水量超过![]() 的家庭大约有多少户?
的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A= ![]() .(注:不要求写作法,但保留作图痕迹)
.(注:不要求写作法,但保留作图痕迹)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
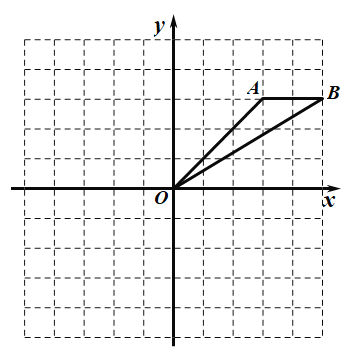
【题目】如图,在平面直角坐标系中,已知点A(3,3),B(5,3).
(1)已知点C(2,-4),求四边形AOCB的面积;
(2)将线段OB先向上平移2个单位长度,再向左平移4个单位长度,得到线段O2B2,画出两次平移后的图形,并求线段OB在两次平移过程中扫过的总面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:求下列事件概率
(1)小杨和小姜住在同一个小区,该小区到苏果超市有A、B、C三条路线.
①求小杨随机选择一条路线,恰好是A路线的概率;
②求小杨和小姜两人分别随机选择一条路线去苏果超市,恰好两人选择同一条路线的概率.
(2)有4位顾客在超市中选购4种品牌的方便面.如果每位顾客从4种品牌中随机的选购一种,那么4位顾客选购同一品牌的概率是 , 至少有2位顾客选择的不是同一品牌的概率是(直接填字母序号)
A. ![]() B.(
B.( ![]() )3 C.1﹣(
)3 C.1﹣( ![]() )3 D.1﹣(
)3 D.1﹣( ![]() )3 .
)3 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com