
 如图,A在O的正北方向,B在O的正东方向,且A、B到点O的距离相等.甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲、乙两人之间的夹角为45°,即∠COD=45°,此时甲、乙两人相距( )
如图,A在O的正北方向,B在O的正东方向,且A、B到点O的距离相等.甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲、乙两人之间的夹角为45°,即∠COD=45°,此时甲、乙两人相距( )| A. | 80千米 | B. | 50$\sqrt{2}$千米 | C. | 100千米 | D. | 100$\sqrt{2}$千米 |
分析 利用旋转的性质结合全等三角形的判定与性质得出△COD≌△B′OC(SAS),则B′C=DC进而求出即可.
解答 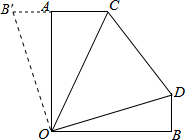 解:由题意可得:AB′=BD=40km,AC=60km,
解:由题意可得:AB′=BD=40km,AC=60km,
将△OBD顺时针旋转270°,则BO与AO重合,
在△COD和△B′OC中
∵$\left\{\begin{array}{l}{DO=OB′}\\{∠COD=∠B′OC}\\{CO=CO}\end{array}\right.$,
∴△COD≌△B′OC(SAS),
则B′C=DC=40+60=100(km),
故选:C.
点评 此题主要考查了勾股定理的应用以及全等三角形的判定与性质,得出△COD≌△B′OC是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
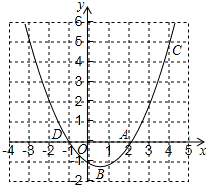 如图,已知二次函数y=$\frac{1}{2}{{x}^{2}}$-$\frac{1}{2}$x-1的图象交x轴于A、D两点.
如图,已知二次函数y=$\frac{1}{2}{{x}^{2}}$-$\frac{1}{2}$x-1的图象交x轴于A、D两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com