
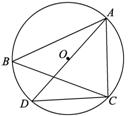
如图28.1-17,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径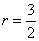 ,AC=2,则cosB的值是( )
,AC=2,则cosB的值是( )
A.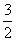
 B.
B.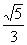 C.
C.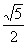 D.
D.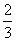
 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
如图,是某公园的一角,∠AOB=90°,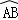 的半径OA长是6米,点C是OA的中点,点D在
的半径OA长是6米,点C是OA的中点,点D在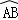 上,CD∥OB,则图中草坪区(阴影部分)的面积是( )
上,CD∥OB,则图中草坪区(阴影部分)的面积是( )

|
| A. | (3π+ | B. | ( | C. | (3π+9 | D. | ( |
查看答案和解析>>
科目:初中数学 来源: 题型:
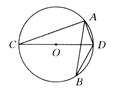
如图3-202所示,CD是⊙O的直径,A,B是⊙O上的两点.若∠ABD=20°,则∠ADC的度数为 ( )
A.40° B.50° C.60° D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
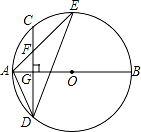
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足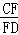 =
=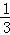 ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)求证:△ADF∽△AE D;
D;
(2)求FG的长;
(3)求证:tan∠E=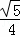 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
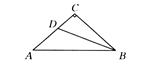
如图1—125所示,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=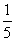 ,则AD的长为 ( )
,则AD的长为 ( )
A.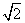 B.2 C.1 D.2
B.2 C.1 D.2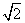
查看答案和解析>>
科目:初中数学 来源: 题型:
某市东坡中学升国旗时,余露同学站在距旗杆底部12 m处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为45°.若她的双眼距地面1.3 m,则旗杆的高度为 m.
查看答案和解析>>
科目:初中数学 来源: 题型:
先请阅读下列题目和解答过程:
“已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:因为a2c2-b2c2=a4-b4①,
所以c2(a2-b2)=(a2+b2)(a2-b2)②,
所以c 2=a2+b2③,
2=a2+b2③,
所以△ABC是直角三角形④.”
请解答下 列问题:
列问题:
( 1)上列解答过程,从第几步到第几步出现错误?
1)上列解答过程,从第几步到第几步出现错误?
(2)简要分析出现错误的原因.
(3)写出正确的解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com