
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
【答案】解:(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,又BF⊥CE,
∴∠CBG+∠BCF=90°,又∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
∴△AEC≌△CGB,
∴AE=CG,
(2)BE=CM,
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵AC=BC,∠ACM=∠CBE=45°,
∴△BCE≌△CAM,
∴BE=CM.
【解析】
⑴证明:设∠ACE=∠1,因为直线BF垂直于CE,交CE于点F,所以∠CFB=90°,
所以∠ECB+∠CBF=90°.
又因为∠1+∠ECB=90°,所以∠1=∠CBF .
因为AC="BC," ∠ACB=90°,所以∠A=∠CBA=45°.
又因为点D是AB的中点,所以∠DCB=45°.
因为∠1=∠CBF,∠DCB=∠A,AC=BC,所以△CAE≌△BCG,所以AE=CG.
(2)解:CM=BE.证明如下:因为∠ACB=90°,所以∠ACH +∠BCF=90°.
因为 CH⊥AM,即∠CHA=90°,所以 ∠ACH +∠CAH=90°,所以∠BCF=∠CAH.
因为 CD为等腰直角三角形斜边上的中线,所以 CD=AD.所以∠ACD=45°.
在△CAM与△BCE中,CA=BC,∠CAH =∠BCF, ∠ACM =∠CBE,
所以 △CAM ≌△BCE,所以CM=BE.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|2a﹣b+8|+(a+b﹣2)2=0.

(1)求a、b的值;
(2)如图1,点G在y轴上,三角形COG的面积是三角形ABC的面积的![]() ,求出点G的坐标;
,求出点G的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一个动点,连接OP、AC、DB,OE平分∠AOP,OF⊥CE,若∠OPD+k∠DOF=k(∠FOP+∠AOE),现将四边形ABDC向下平移![]() k个单位得到四边形A1B1D1C1,已知AM+BN =
k个单位得到四边形A1B1D1C1,已知AM+BN =![]() k,求图中阴影部分的面积.
k,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商场有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑,某中学准备从甲、乙两种品牌的电脑中各选购一种型号的电脑安装到各班教室.
(1)写出所有选购方案(利用树状图或列表法表示);
(2)若(1)中各种选购方案被选中的可能性相同,那么A型号被选中的概率是多少?
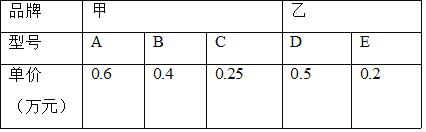
(3)已知该中学用18万元人民币购买甲、乙两种品牌电脑刚好32台(价格如下表所示,单位:万元),其中甲品牌电脑选为A型号,求该中学购买到A型号电脑多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
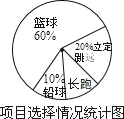
【题目】光明中学七年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
项目选择情况统计图训练后篮球定时定点投篮测试进球数统计表
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)选择长跑训练的人数占全班人数的百分比是_____%,该班共有同学_____人;
(2)求训练后篮球定时定点投篮人均进球数;
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%.请求出参加训练之前的人均进球数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四块完全相同的小长方形拼成的一个“回形”正方形.

(1)用不同代数式表示图中的阴影部分的面积,你能得到怎样的等式:________;
(2)利用(1)中的结论.计算:![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)根据(1)的结论.若![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
(1)P点的坐标为多少;(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发向点
出发向点![]() 运动,运动到点
运动,运动到点![]() 停止,同时,点
停止,同时,点![]() 从点
从点![]() 出发向点
出发向点![]() 运动,运动到点
运动,运动到点![]() 即停止,点
即停止,点![]() 、
、![]() 的速度都是每秒1个单位,连接
的速度都是每秒1个单位,连接![]() 、
、![]() 、
、![]() .设点
.设点![]() 、
、![]() 运动的时间为
运动的时间为![]() 秒
秒
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 是矩形;
是矩形;
(2)当![]() 时,判断四边形
时,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com