
【题目】如图,在等腰直角![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为直角顶点做等腰直角
为直角顶点做等腰直角![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的度数为( )
的度数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
如图,在MN上截取MH=NQ,由“SAS”可证△DFM≌△DEN,△DMH≌△DNQ可得∠DEN=∠DFM=45°,DH=DQ,可证△DHQ是等边三角形,由三角形内角和可求解.
如图,在MN上截取MH=NQ,

∵△DEF和△DNM是等腰直角三角形,
∴DE=DF,DM=DN,∠FDE=∠MDN=90°,
∴∠DEF=∠DFE=∠DMN=∠DNM=45°,
∵∠FDE=∠MDN=90°,
∴∠MDF=∠NDE,且DF=DE,DM=DN,
∴△DFM≌△DEN(SAS),
∴∠DFM=∠DEN=45°,
∵DM=DE,∠DMN=∠DNM,MH=NQ,
∴△DMH≌△DNQ(SAS),
∴DH=DQ,
∵MQ=DQ+NQ,且MQ=MH+HQ,
∴DQ=HQ,
∴DH=DQ=HQ,
∴△DHQ是等边三角形,
∴∠DQH=60°=∠NQE,
∴∠MNE=180°-∠QNE-∠QEN=75°,
故选:B.


科目:初中数学 来源: 题型:
【题目】有下列命题:①两条直线被第三条直线所截,同位角相等;②0.1的算术平方根是0.01;③算术平方根等于它本身的数是1;④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1;⑤若a2=b2,则a=b;⑥若![]() =
=![]() ,则a=b.其中假命题的个数是( )
,则a=b.其中假命题的个数是( )
A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象为直线
的图象为直线![]() ,函数
,函数![]() 的图象为直线
的图象为直线![]() ,直线
,直线![]() 、
、![]() 分别交
分别交![]() 轴于点
轴于点![]() 和点
和点![]() ,分别交
,分别交![]() 轴于点
轴于点![]() 和
和![]() ,
,![]() 和
和![]() 相交于点
相交于点![]()
(1)填空:![]() ;求直线
;求直线![]() 的解析式为 ;
的解析式为 ;
(2)若点![]() 是
是![]() 轴上一点,连接
轴上一点,连接![]() ,当
,当![]() 的面积是
的面积是![]() 面积的2倍时,请求出符合条件的点
面积的2倍时,请求出符合条件的点![]() 的坐标;
的坐标;
(3)若函数![]() 的图象是直线
的图象是直线![]() ,且
,且![]() 、
、![]() 、
、![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是正
是正![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心逆时针旋转60°得到线段
为旋转中心逆时针旋转60°得到线段![]() ,下列结论:①
,下列结论:①![]() 可以由
可以由![]() 绕点
绕点![]() 逆时针旋转60°得到;②点
逆时针旋转60°得到;②点![]() 与
与![]() 的距离为6;③
的距离为6;③![]() ;④
;④![]() ;⑤
;⑤![]()
![]() .其中正确的结论是(填序号)______.
.其中正确的结论是(填序号)______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
计算方差的公式:s2=![]() [(x1-
[(x1-![]() )2+(x2-
)2+(x2-![]() )2++(xn-
)2++(xn-![]() )2]
)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示,设边框的宽为xcm,如果整个挂图的面积是5400cm2 ,那么下列方程符合题意的是( )
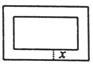
A. (50-x)(80-x)=5400 B. (50-2x)(80-2x)=5400
C. (50+x)(80+x)=5400 D. (50+2x)(80+2x)=5400
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=55°,求∠BOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com