
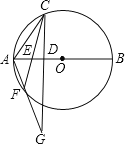
【题目】已知,如图,AB是![]() 的直径,C是
的直径,C是![]() 上一点,连接AC,过点C作直线
上一点,连接AC,过点C作直线![]() 于D(
于D(![]() ),点E是DB上任意一点(点D、B除外),直线CE交
),点E是DB上任意一点(点D、B除外),直线CE交![]() 于点F.连接AF与直线CD交于点G.
于点F.连接AF与直线CD交于点G.
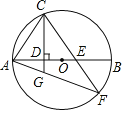
(1)求证:![]()
(2)若点E是AD(点A除外)上任意一点,上述结论是否仍然成立?若成立,请画出图形并给予证明;若不成立,请说明理由。
【答案】(1)证明见解析;(2)成立,证明见解析.
【解析】
(1)欲证AC2=AGAF,即证AC:AG=AF:AC,可以通过证明△AGC∽△ACF得到;
(2)分清E点在AD上有两种情况,然后逐一证明.
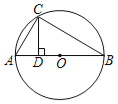
(1)证明:连接CB,
∵AB是直径,CD⊥AB,
∴∠ACB=∠ADC=90°,又∠CAD=∠BAC,
∴△CAD∽△BAC,
∴∠ACD=∠ABC,
∵∠ABC=∠AFC,
∴∠ACD=∠AFC,∠CAG=∠FAC,
∴△ACG∽△AFC,
∴![]() ,
,
∴AC2=AGAF;
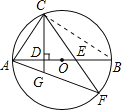
(2)当点E是AD(点A除外)上任意一点,上述结论仍成立
①当点E与点D重合时,F与G重合,如图所示:
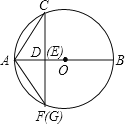
有AG=AF,∵CD⊥AB,
∴![]() ,AC=AF,
,AC=AF,
∴AC2=AGAF;
②当点E与点D不重合时(不含点A)时,如图所示:
证明类似(1).


科目:初中数学 来源: 题型:
【题目】已知:线段MN=a.
![]()
(1)求作:边长为![]() a的正三角形ABC.(要求:尺规作图,不写作法但保留作图痕迹)
a的正三角形ABC.(要求:尺规作图,不写作法但保留作图痕迹)
(2)若a=10cm.求(1)中正三角形ABC的内切圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
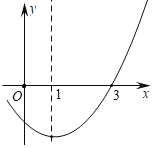
【题目】若二次函数y=x2﹣2x+k的部分图象如图所示,则关于x的一元二次方程x2﹣2x+k=0的解一个为x1=3,则方程x2﹣2x+k=0另一个解x2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图乙,![]() 和
和![]() 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形,![]() ,点P为射线BD,CE的交点.
,点P为射线BD,CE的交点.
![]() 如图甲,将
如图甲,将![]() 绕点A旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是______.
绕点A旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是______.
![]()
![]() 若
若![]() ,
,![]() ,把
,把![]() 绕点A旋转,
绕点A旋转,
![]() 当
当![]() 时,求PB的长;
时,求PB的长;
![]() 求旋转过程中线段PB长的最大值.
求旋转过程中线段PB长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
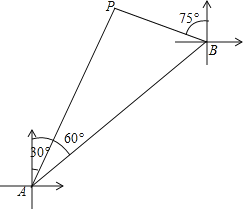
【题目】如图,一艘轮船在A处测得灯塔P在船的北偏东30°方向,轮船沿着北偏东60°方向航行16km后到达B处,这时灯塔P在船的北偏西75°方向.则灯塔P与B之间的距离等于___________km(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
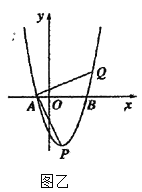
【题目】如图甲,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,且三个垂足在同一直线上.
,且三个垂足在同一直线上.
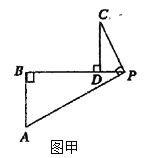
(1)证明:![]() ;
;
(2)已知地物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,如图乙所示,若
,如图乙所示,若![]() 是抛物线上异于
是抛物线上异于![]() 的点,使得
的点,使得![]() ,求
,求![]() 点坐标(提示:可结合第(1)小题的思路解答)
点坐标(提示:可结合第(1)小题的思路解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省第十五届运动会乒乓球比赛于2018年8月13日上午在山西省体育博物馆的比赛场馆内正式拉开了帷幕.第十五届运动会竞技体育组乒乓球项目产生的决赛运动员名单中太原市共27人,其中甲组有甲、乙、丙、丁四名女子运动员,若进行一次乒乓球单打比赛,要通过抽签从中选出两名运动员打第一场比赛.
(1)若已确定甲打第一场,再从其余三名运动员中随机选取一位,求恰好选中乙的概率;
(2)若两名运动员都不确定,请用树状图法或列表法,求恰好选中甲、乙两名运动员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条抛物线![]() 与
与![]() 的两个交点
的两个交点![]() 、
、![]() 都在
都在![]() 轴上,抛物线
轴上,抛物线![]() 的顶点为
的顶点为![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)在![]() 轴正半轴上有一点
轴正半轴上有一点![]() ,当
,当![]() 时,求
时,求![]() 的面积;
的面积;
(3)判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使点
,使点![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到点
,得到点![]() 恰好落在抛物线
恰好落在抛物线![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
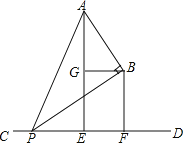
【题目】综合与实践:
操作与发现:
如图,已知A,B两点在直线CD的同一侧,线段AE,BF均是直线CD的垂线段,且BF在AE的右边,AE=2BF,将BF沿直线CD向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线CD相交于点P,点G是AE的中点,连接BG.
探索与证明:求证:
(1)四边形EFBG是矩形;
(2)△ABG∽△PBF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com