
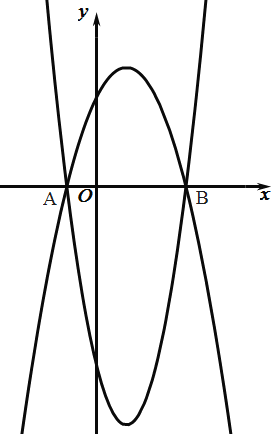
【题目】两条抛物线![]() 与
与![]() 的两个交点
的两个交点![]() 、
、![]() 都在
都在![]() 轴上,抛物线
轴上,抛物线![]() 的顶点为
的顶点为![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)在![]() 轴正半轴上有一点
轴正半轴上有一点![]() ,当
,当![]() 时,求
时,求![]() 的面积;
的面积;
(3)判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使点
,使点![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到点
,得到点![]() 恰好落在抛物线
恰好落在抛物线![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)存在;点P坐标为:
;(3)存在;点P坐标为:![]() 或
或![]() .
.
【解析】
(1)利用抛物线![]() ,求出点A、B的坐标,然后用待定系数法求出
,求出点A、B的坐标,然后用待定系数法求出![]() 的解析式即可;
的解析式即可;
(2)根据题意,可分两种情况进行讨论,①在抛物线的对称轴上取一点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作圆,与y轴正半轴有交点
为半径作圆,与y轴正半轴有交点![]() ,根据勾股定理求出点
,根据勾股定理求出点![]() 坐标,然后求出面积;②在
坐标,然后求出面积;②在![]() 轴下方抛物线的对称轴上,取一点
轴下方抛物线的对称轴上,取一点![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作圆,与y的正半轴有交点
为半径作圆,与y的正半轴有交点![]() ,通过计算,
,通过计算,![]() 不符合题意,最后即可得到
不符合题意,最后即可得到![]() 的面积;
的面积;
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,分两种情况进行讨论:①当点
,分两种情况进行讨论:①当点![]() 在点
在点![]() 上方时,设
上方时,设![]() ,先证明
,先证明![]() ,然后利用方程的思想求出
,然后利用方程的思想求出
![]() 的值,然后得到点P的坐标;②当点
的值,然后得到点P的坐标;②当点![]() 在点
在点![]() 下方时,设
下方时,设![]() ,与①同理可证
,与①同理可证![]() ,然后利用方程的思想求出z的值,得到点P的坐标.
,然后利用方程的思想求出z的值,得到点P的坐标.
解:(1)∵点![]() ,
,![]() 都在
都在![]() 轴上,
轴上,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
把点![]() ,
,![]() 代入
代入![]() 得,
得,
![]()
解得:![]() ,
,
∴![]() .
.
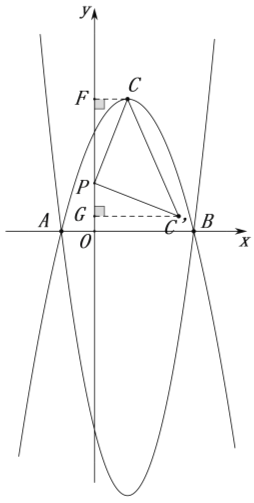
(2)如图,抛物线的对称轴与![]() 轴交点为
轴交点为![]()
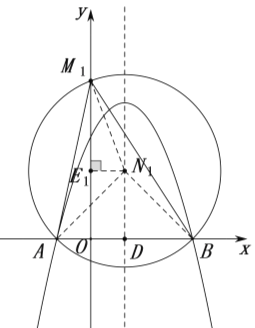
![]() ,
,![]()
∴![]() .
.
①如图,在![]() 轴上方抛物线的对称轴上,取一点
轴上方抛物线的对称轴上,取一点![]() ,使
,使![]()
![]() ,
,![]() ,
,
![]() ,
,
以点![]() 为圆心,以
为圆心,以![]() 为半径作圆,
为半径作圆,
与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,即:
,即:![]() ,
,
![]() .
.
设点![]() (
(![]() ),过点
),过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() ,
,![]() (舍去),
(舍去),
![]()
![]() .
.
②如图,在![]() 轴下方抛物线的对称轴上,取一点
轴下方抛物线的对称轴上,取一点![]() ,使
,使![]()
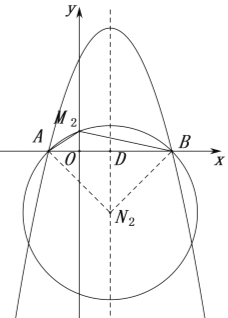
![]() ,
,![]() ,
,
![]() ,
,
以点![]() 为圆心,以
为圆心,以![]() 为半径作圆,
为半径作圆,
与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,即:
,即:![]() ,舍去.
,舍去.
![]() 的面积为:
的面积为:![]() .
.
(3)![]() ,顶点
,顶点![]() ,
,
如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
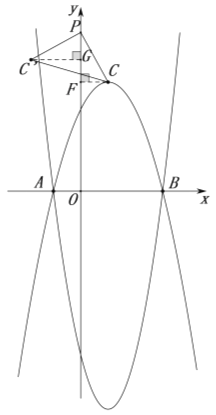
①当点![]() 在点
在点![]() 上方时,设
上方时,设![]() ,依题意得:
,依题意得:
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,![]()
![]()
![]() 恰好落在抛物线
恰好落在抛物线![]() 上,
上,
![]()
∴![]() (舍去)
(舍去)
![]() .
.
②当点![]() 在点
在点![]() 下方时,设
下方时,设![]() ,
,
同理可证:![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() 恰好落在抛物线
恰好落在抛物线![]() 上,
上,
![]()
![]() ,
,![]() (舍去)
(舍去)
![]() .
.
综上所述,![]() ,
,![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是![]() 的直径,C是
的直径,C是![]() 上一点,连接AC,过点C作直线
上一点,连接AC,过点C作直线![]() 于D(
于D(![]() ),点E是DB上任意一点(点D、B除外),直线CE交
),点E是DB上任意一点(点D、B除外),直线CE交![]() 于点F.连接AF与直线CD交于点G.
于点F.连接AF与直线CD交于点G.
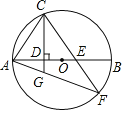
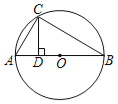
(1)求证:![]()
(2)若点E是AD(点A除外)上任意一点,上述结论是否仍然成立?若成立,请画出图形并给予证明;若不成立,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )

A. AE∥BD B. AB=BF C. AF∥CD D. DF=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D、E分别是BC和CB延长线上的点,且![]() ,连接AD、AE,BM、CN分别是△ABE和△ACD的高线,垂足分别为M、N, BG、CH分别是∠ABE和∠ACD的平分线,分别交AE、AD于点G、H.
,连接AD、AE,BM、CN分别是△ABE和△ACD的高线,垂足分别为M、N, BG、CH分别是∠ABE和∠ACD的平分线,分别交AE、AD于点G、H.
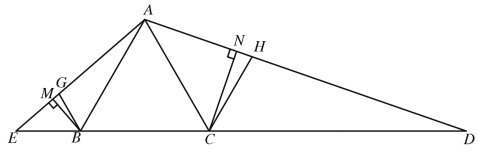
证明:(1)△ABE∽△DCA;
(2)sin∠MBG=sin∠NCH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房![]() 间供游客居住,当每间客房的定价为每天
间供游客居住,当每间客房的定价为每天![]() 元时,客房恰好全部住满;如果每间客房每天的定价每增加
元时,客房恰好全部住满;如果每间客房每天的定价每增加![]() 元,就会减少
元,就会减少![]() 间客房出租.设每间客房每天的定价增加
间客房出租.设每间客房每天的定价增加![]() 元,宾馆出租的客房为
元,宾馆出租的客房为![]() 间.求:
间.求:
![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 如果某天宾馆客房收入
如果某天宾馆客房收入![]() 元,那么这天每间客房的价格是多少元?
元,那么这天每间客房的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
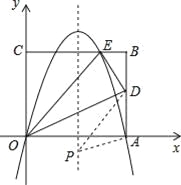

(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
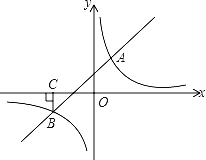
(1)求反比例函数的解析式;
(2)过B点作BC⊥x轴,垂足为C,若P是反比例函数图象上的一点,连接PC,PB,求当△PCB的面积等于5时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com