
【题目】综合与实践:
操作与发现:
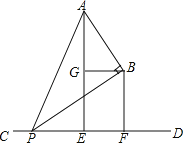
如图,已知A,B两点在直线CD的同一侧,线段AE,BF均是直线CD的垂线段,且BF在AE的右边,AE=2BF,将BF沿直线CD向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线CD相交于点P,点G是AE的中点,连接BG.
探索与证明:求证:
(1)四边形EFBG是矩形;
(2)△ABG∽△PBF.
【答案】(1)见解析;(2)见解析.
【解析】
(1)先通过等量代换得出GE=BF,然后由AE⊥CD,BF⊥CD得出AE∥BF,从而得到四边形EFBG是平行四边形,最后利用BF⊥CD,则可证明平行四边形EFBG是矩形;
(2)先通过矩形的性质得出∠AGB=∠GBF=∠BFE=90°,然后通过等量代换得出∠ABG=∠PBF,再加上∠AGB=∠PFB=90°即可证明△ABG∽△PBF.
(1)证明:∵AE⊥CD,BF⊥CD,
∴AE∥BF,
∵AE=2BF,
∴BF=![]() AE,
AE,
∵点G是AE的中点,
∴GE=![]() AE,
AE,
∴GE=BF,又AE∥BF,
∴四边形EFBG是平行四边形,
∵BF⊥CD,
∴平行四边形EFBG是矩形;
(2)∵四边形EFBG是矩形,
∴∠AGB=∠GBF=∠BFE=90°,
∵∠ABP=90°,
∴∠ABP﹣∠GBP=∠GBF﹣∠GBP,
即∠ABG=∠PBF,
∵∠ABG=∠PBF,∠AGB=∠PFB=90°,
∴△ABG∽△PBF.


科目:初中数学 来源: 题型:
【题目】已知,如图,AB是![]() 的直径,C是
的直径,C是![]() 上一点,连接AC,过点C作直线
上一点,连接AC,过点C作直线![]() 于D(
于D(![]() ),点E是DB上任意一点(点D、B除外),直线CE交
),点E是DB上任意一点(点D、B除外),直线CE交![]() 于点F.连接AF与直线CD交于点G.
于点F.连接AF与直线CD交于点G.
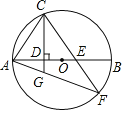
(1)求证:![]()
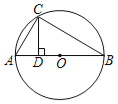
(2)若点E是AD(点A除外)上任意一点,上述结论是否仍然成立?若成立,请画出图形并给予证明;若不成立,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房![]() 间供游客居住,当每间客房的定价为每天
间供游客居住,当每间客房的定价为每天![]() 元时,客房恰好全部住满;如果每间客房每天的定价每增加
元时,客房恰好全部住满;如果每间客房每天的定价每增加![]() 元,就会减少
元,就会减少![]() 间客房出租.设每间客房每天的定价增加
间客房出租.设每间客房每天的定价增加![]() 元,宾馆出租的客房为
元,宾馆出租的客房为![]() 间.求:
间.求:
![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 如果某天宾馆客房收入
如果某天宾馆客房收入![]() 元,那么这天每间客房的价格是多少元?
元,那么这天每间客房的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
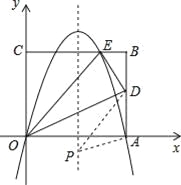

(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树状图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在直线y=﹣x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
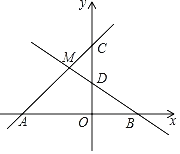
【题目】如图,直线y=x+3分别与x轴、y轴交于点A、C,直线y=mx+![]() 分别与x轴、y轴交于点B、D,直线AC与直线BD相交于点M(﹣1,b)
分别与x轴、y轴交于点B、D,直线AC与直线BD相交于点M(﹣1,b)
(1)不等式x+3≤mx+![]() 的解集为 .
的解集为 .
(2)求直线AC、直线BD与x轴所围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).
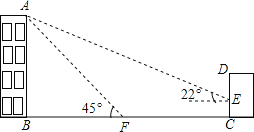
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22≈![]() ,cos22≈
,cos22≈![]() ,tan22≈
,tan22≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
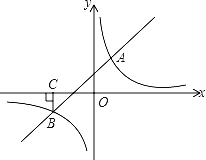
(1)求反比例函数的解析式;
(2)过B点作BC⊥x轴,垂足为C,若P是反比例函数图象上的一点,连接PC,PB,求当△PCB的面积等于5时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com